算法学习笔记 -- Dancing Links

Coast23
  2025-07-01 11:09:43 2025-07-01 11:09:43 创建   2025-07-03 14:11:54 2025-07-03 14:11:54 更新    2.9k 字  12 分钟  

前言

在爆搜数独题 TLE 之后, 得知了基于 Dancing Links 的 X Algorithm, 感觉非常有意思, 遂记录之.

论文出处: arXiv:cs/0011047

参考资料: OI Wiki

网上一搜一大把相关内容.

问题引入

洛谷P4929

给定一个行列的矩阵，矩阵中每个元素要么是，要么是。

你需要在矩阵中挑选出若干行，使得对于矩阵的每一列，在你挑选的这些行中，有且仅有一行的第个元素为。

输出顺序任意, 若无解，输出 No Solution!。

数据范围:,保证矩阵中的数量不超过个。

思路

很容易想到这样的深搜做法 (也很符合正常人的思维):

    1. 对于其中一列, 枚举这一列含 1 的每一行, 并假设我选择了, 显然可能不止在列上含有 1, 我就再遍历的每一列含 1 的行, 把删掉. (删掉表示这一列已经有 1 了, 不能再选了)
    1. 删了, 就接着往下搜 (考虑其它列).
    1. 接着考虑回溯, 也就是恢复我们刚刚删掉的行, 再去考虑选其它行.
    1. 终止条件为: 搜索到最后所有行都删完了 (无冲突, 有解), 或者发现到最后有删不掉的行 (有冲突, 无解).

显然, 每层搜索中列是必删的. 那么应该如何选择列呢? 是不是随便选一列就行?

当然可以, 但如果我们每次都选择含 1 最少的列作为列, 那么搜索的分支就最少, 效率也会大大提高. (启发式搜索)

思路有了, 问题在于如何高效地实现这个 删除 与 恢复 操作.

于是, 大牛 Donald E. Knuth 就联想到了双向链表的删除操作:

// 假设 p 的前驱为 left, 后继为 right, 且都不为空
void remove(Node* p){
    p->left->right = p->right;
    p->right->left = p->left; // 这两行是把 p 的前驱和后继直接相连
    delete p; // 然后删除 p ?
}

但实际上, 如果我们不删除掉的话, 我们就可以通过:

void recover(Node* p){
    // 在删除操作中, 我们仅分别改变了 p->left 和 p->right 这两个结点的后继和前驱,
    // 实际上, p->left 和 p->right 仍然指向原来的位置.
    p->left->right = p;
    p->right->left = p; // 这样就成功把 p 插入到 p->left 和 p->right 之间了!
}

哎! 那不就可以利用这个, 实现我们想要的 删除 与 恢复 操作了吗?

再回头看看我们的需求:

  • 选中一列 (选择处理一个约束), 遍历这个列中含 1 的每一行:
    • 对于每个元素, 既能在行上遍历, 也能在列上遍历, 也就是说它得是个 十字形链表.
  • 我们知道链表的遍历是朝一个方向进行的, 如果从节点往后遍历, 要如何遍历到它的前驱呢?
    • 最简单的解决方式, 就是让这个链表是 双向环状 的, 把链表第一个元素和最后一个元素相连.

OK, 现在我们选择了 双向十字循环链表 作为我们的辅助数据结构, 那这个 链表 应该如何构造?

build

不难想到, 我们可以先创造一行个元素, 每个元素表示第列的头节点, 然后把这个元素在水平方向上串起来, 也就是说, 我们先创建了一个像这样的表格的 固定表头 (第一行):

012…m
无||…|
无|…|
无||…
无|…|

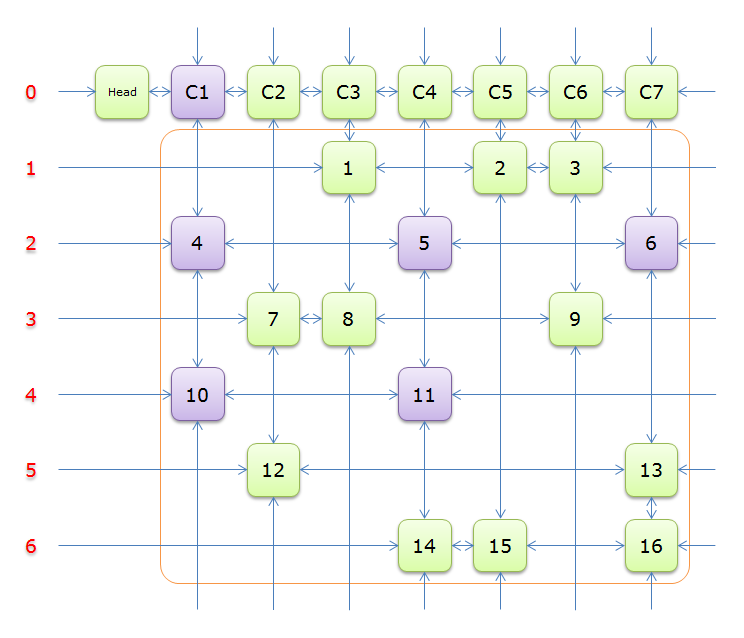
或者看这张图, 更直观. (图片来源于网络)

1.png

wait, 不是说创造个元素吗? 为什么有第列?

这个第列的设计相当巧妙, 初始时,的 left 为, right 为. 随着删除的进行, 始终保持有的 right 为第一个待删除的列, 且当所有列都删完时有的 left 和 right 都指向自己 (), 可以方便地判断是否已经删完.

于是就可以给出 build 函数了:

struct DLX{
    int n, m, tot;     // n 行, m 列, 已经创建了 tot 个节点
	int size[MAX_C + 1]; // 指示每列的节点数 (不含头节点)
	int up[SIZE], down[SIZE], left[SIZE], right[SIZE];
    // 编号为 i 的节点的上、下、左、右的节点编号

    // 创建一个 r 行 c 列的表, 初始化其列表头
    void build(const int &r, const int &c){
        n = r, m = c;
        for(int i = 0; i <= c; ++i){ // 令表头在总节点的编号中为 0~c
            left[i] = i - 1, right[i] = i + 1;
            up[i] = down[i] = i;
        }
        left[0] = c, right[c] = 0; // 0号节点要特殊处理
        tot = c; // tot 指示最后一个被创建的节点的编号
        memset(size, 0, sizeof(size)); // 给列大小 清零
    }
};

创建完列表头了, 接下来就要思考如何往第行, 第列插入节点.

insert

wait, 我们只创建了列表头, 行表头去哪了?

嗯, 我们不需要固定的行表头.

别忘了我们的目标, 我们只需要能够遍历第行的所有节点就行了, 由于行链表是双向环状的, 我们只需要找到第行的一个节点就能遍历整个行. 换言之, 第行的每个点都能成为 “头节点”, 不妨取第一个插入进行的元素为这个“头节点”, 我们将之称为 哨兵节点, 用 first[r] 表示.

现在我们来思考如何向第行, 第列插入节点.

先说往第列插入, 这个简单, 只需要在第列的头节点下面插入即可, 是简单的链表插入.

// 新建一个节点, 把它插入到第 c 列的头节点的后面
++tot;
// ++tot 是新节点的编号, 而 c 就是第 c 列的头节点的编号
down[tot] = down[c], up[tot] = c;
up[down[c]] = tot, down[c] = tot;

再说往第行插入, 这个需要分类讨论:

  • 如果第行还没有节点, 那么这个新的节点就要成为这一行的头节点:
// first[r] 及其前驱后继都是 tot
if(!first[r]) first[r] = left[tot] = right[tot] = tot;
  • 如果第行已经有节点了, 那就和插入到列一样, 把它插入到哨兵节点的右边:
if(first[r]){
    left[tot] = first[r];
    right[tot] = right[first[r]];

    left[right[first[r]]] = tot;
    right[first[r]] = tot;
}

整合一下, 得到 insert 函数:

struct DLX{
    int n, m, tot;
    int col[SIZE], raw[SIZE]; // 编号为 i 的节点的列编号, 行编号
	int first[MAX_R + 1];     // 第 i 行的哨兵节点
    int size[MAX_C + 1];
	int up[SIZE], down[SIZE], left[SIZE], right[SIZE];

    void insert(const int &r, const int &c){
        // 新建节点, 标记其行列, 记得给第 c 列的节点数加 1
        raw[++tot] = r, col[tot] = c, ++size[c];
        // 往 c 列的头节点的下面插入
        down[tot] = down[c], up[tot] = c;
        up[down[c]] = tot, down[c] = tot;
        // 如果 r 行还没有节点, 就成为 r 行的第一个节点
        if(!first[r]) first[r] = left[tot] = right[tot] = tot;
        // 否则插入到 r 行的哨兵节点的右边
        else{
            left[tot] = first[r];
            right[tot] = right[first[r]];

            left[right[first[r]]] = tot;
            right[first[r]] = tot;
        }
    }
};

remove & recover

build 和 insert 应该是最难理解的部分了, 接下来就是实现删除、恢复第列的 remove 和 recover 函数, 直接看代码和注释就懂了.

struct DLX{
    int n, m, tot;
    int col[SIZE], raw[SIZE];
	int first[MAX_R + 1], size[MAX_C + 1];
	int up[SIZE], down[SIZE], left[SIZE], right[SIZE];

    void remove(const int &c){
        // "删掉"第 c 列的表头节点
        right[left[c]] = right[c], left[right[c]] = left[c];
        // 接下来往下遍历第 c 列的所有元素 (其实往上也行, 环嘛, 都一样)
        for(int i = down[c]; i != c; i = down[i]){
            // 删掉在第 c 列的节点 i 的所在行, 因为这一行不可能进入决策了
            // 遍历 i 所在行的元素 j, 把 up[j] 和 down[j] 连起来
            for(int j = right[i]; j != i; j = right[j]){
                down[up[j]] = down[j], up[down[j]] = up[j];
                --size[col[j]]; // 别忘了: j 所在列的节点数要减 1
            }
        }
    }

    void recover(const int &c){
        // 和 remove 完全相反的操作
        for(int i = up[c]; i != c; i = up[i]){
            for(int j = left[i]; j != i; j = left[j]){
                down[up[j]] = up[down[j]] = j, ++size[col[j]];
            }
        }
        // 恢复第 c 列的表头节点
        right[left[c]] = left[right[c]] = c;
    }
};

Let’s dance!

接下来, 就可以实现 dfs 了, 也就是 dance 函数.

思路在最开始就讲了, 所以直接上代码.

int stackl[MAX_R + 1]; // 记录选择的行
struct DLX{
    // ... 其它部分
    bool dance(int step){ // step 表示已经删了几行
        if(!right[0]){    // 0 号节点的 right 指针指向自己, 说明已经删完了
            for(int i = 0; i < step; ++i)
                printf("%d ", stack[i]);
            return true; // 直接输出选中的行, 并返回 true 表示找到解
        }
        // 启发式搜索: 选择删掉 size 最小的列 c
        int c = right[0];
        for(int i = right[0]; i; i = right[i]){
            if(size[i] < size[c]) c = i;
        }
        // 这句话的意思是, 没有行能够满足列 c了, 因此目前的方案不可行.
        if(size[c] == 0) return false;

        // 删掉列 c, 并遍历在列 c 上的行, 删掉它们的列
        remove(c);
        for(int i = down[c]; i != c; i = down[i]){
            stack[step] = raw[i]; // 为了删掉列 c, 我们选择这一行, 删掉其它行
            for(int j = right[i]; j != i; j = right[j]) remove(col[j]);
            if(dance(step + 1)) return true; // 递归往下搜, 有解了就返回 true
            for(int j = left[i]; j != i; j = left[j]) recover(col[j]); // 回溯
        }
        recover(c); // 回溯
        return false; // 能执行到这里, 就说明目前的方案不可行.
    }
};

其它上面没提的事项

  • 因为我们只关心 1, 不关心 0, 所以我们只插入 1 节点.
  • 既然只插入 1 节点, 那么 SIZE 就是 1 的数量.
  • MAX_C 表示约束的数量, MAX_R 表示可选择的方案数.
  • 因此, 可以把某些问题 (如数独) 转化为 精确覆盖问题, 然后用 DLX 解决.

完整模板

#include <cstdio>
#include <cstring>
#include <iostream>

const int MAX_C = 501;
const int MAX_R = 501;
const int SIZE = MAX_C + 5001;
int stack[SIZE];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
    return f ? x : -x;
}

struct DLX{
    int n, m, tot;
    int col[SIZE], raw[SIZE];
	int first[MAX_R + 1], size[MAX_C + 1];
	int up[SIZE], down[SIZE], left[SIZE], right[SIZE];

    void build(const int &r, const int &c){
        n = r, m = c;
        for(int i = 0; i <= c; ++i){
            left[i] = i - 1, right[i] = i + 1;
            up[i] = down[i] = i;
        }
        left[0] = c, right[c] = 0;
        tot = c;
        memset(size, 0, sizeof(size));
    }

    void remove(const int &c){
        right[left[c]] = right[c], left[right[c]] = left[c];
        for(int i = down[c]; i != c; i = down[i]){
            for(int j = right[i]; j != i; j = right[j]){
                down[up[j]] = down[j], up[down[j]] = up[j];
                --size[col[j]];
            }
        }
    }

    void recover(const int &c){
        for(int i = up[c]; i != c; i = up[i]){
            for(int j = left[i]; j != i; j = left[j]){
                down[up[j]] = up[down[j]] = j, ++size[col[j]];
            }
        }
        right[left[c]] = left[right[c]] = c;
    }

    void insert(const int &r, const int &c){
        raw[++tot] = r, col[tot] = c, ++size[c];
        down[tot] = down[c], up[tot] = c;
        up[down[c]] = tot, down[c] = tot;
        if(!first[r]) first[r] = left[tot] = right[tot] = tot;
        else{
            left[tot] = first[r];
            right[tot] = right[first[r]];

            left[right[first[r]]] = tot;
            right[first[r]] = tot;
        }
    }
    bool dance(int step){
        if(!right[0]){
            for(int i = 0; i < step; ++i)
                printf("%d ", stack[i]);
            return true;
        }
        int c = right[0];
        for(int i = right[0]; i; i = right[i]){
            if(size[i] < size[c]) c = i;
        }
        if(size[c] == 0) return false;
        remove(c);
        for(int i = down[c]; i != c; i = down[i]){
            stack[step] = raw[i];
            for(int j = right[i]; j != i; j = right[j]) remove(col[j]);
            if(dance(step + 1)) return true;
            for(int j = left[i]; j != i; j = left[j]) recover(col[j]);
        }
        recover(c);
        return false;
    }
}solver;

int main(){
    int n, m;
    n = read(), m = read();
    solver.build(n, m);
    for(int i = 1; i <= n; ++i){
        for(int j = 1; j <= m; ++j){
            int x = read();
            if(x) solver.insert(i, j);
        }
    }
    if(!solver.dance(0)) puts("No Solution!");
}
  • 标题: 算法学习笔记 -- Dancing Links
  • 作者: Coast23
  • 创建于 : 2025-07-01 11:09:43
  • 更新于 : 2025-07-03 14:11:54
  • 链接: https://coast23.github.io/2025/07/01/算法学习笔记-Dancing-Links/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
目录
算法学习笔记 -- Dancing Links
  1. 前言
  2. 问题引入
  3. 思路
  4. Dancing Links 的引入
  5. Dancing Links 的构造
    1. build
    2. insert
    3. remove & recover
  6. Let’s dance!
  7. 其它上面没提的事项
  8. 完整模板