程序设计实践 Week2 解题记录

程序设计实践 Week2 解题记录

Coast23
  2025-07-03 11:30:37 2025-07-03 11:30:37 创建   2025-07-03 14:16:59 2025-07-03 14:16:59 更新   10.6k 字  53 分钟  

前言

Week 2 的题目强度略大, 到周三才推完.

光是学习 Dancing Links 就花了大半天时间.

和 Week 1 不一样, 刷完 Week 2 的题后是真的挺有成就感.

1. 英杰们的蛋糕塔

传送门 -- 洛谷 P1731 [NOI1999] 生日蛋糕

题意简述

给定两个个整数和, 请你构造层叠在一起的圆柱体, 满足:

  1. 从下往上, 圆柱体的半径与高均严格递减.
  2. 圆柱体的总体积等于.

在满足上述条件下, 最小化这层圆柱体的表面积 (不含底面积), 也就是最小化 所有圆柱体的侧面积之和 + 最大圆柱体的底面积. 记表面积为, 输出即可.

数据范围:.

Solution

搜索题.

为了便于描述, 我接下来说的 体积、面积, 都是指除以后的部分.

从下往上搜和从上往下搜应该都可行, 我选择了前者.

既然是搜索, 对于每一层, 我们都需要去尝试所有可能的和的组合, 然后进入下一层搜索.

显然和的组合越多, 搜索所需要的时间就多, 因此, 最重要的工作就是: 尽可能缩小当前层可选的和的范围.

所谓缩小范围, 就是明确和的上下限.

假设当前层数为, 已经凑出的体积和面积分别为,, 上一层的和分别为和.

根据半径和高都递减的条件, 首先肯定有:,.
再假设第行半径和高都为, 第行半径和高为,, 第行半径和高都为, 很容易发现.

这个范围还是太大了, 为了进一步缩小和的范围, 自然想到利用体积放缩 .

凑出上面每层所需最小体积

而 “凑出上面每层所需最小体积” 就是, 第一层半径和高都为, 第二层半径和高为,, 第层半径和高都为, 累和起来得到的体积.

把 “凑出前层所需最小体积” 记为 min_v[i], 显然这个时候它们贡献的侧面积也最小, 记为 min_s[i] , 它们的计算方式为:

   for(int i = 1; i <= m; ++i){
       min_s[i] = min_s[i-1] + (i * i << 1);
	min_v[i] = min_v[i-1] + (i * i * i);
}

接下来考虑剪枝.

  1. 如果 V + min_v[dep] > n , 说明不可能凑出体积, 剪. (可行性剪枝)
  2. 如果 S + 剩下能凑出的最小面积 >= ans , 说明这种情况不可能比答案更优, 剪. (最优性剪枝)

首先, 剩下能凑出的面积 有个稳定的下界: min_s[dep].
其次, 由数学知识容易知道, 在已知剩下部分的体积的情况下, 我们可以估算出剩下部分的最小侧面积.

再把放缩为常数利用有

然后, 就是 DFS 入口的确定, 也就是估计第层的和的上限.

这里我一开始以为要二分 , 但还是先考虑了如下非常宽松的情况:

  • 令得到的一个上界.
  • 令得到的一个上界.

还好, 这样就能通过.

公式的推导都写得很详尽了, 代码就不给注释了.

AC Code:

/*
\sum{R^2 * H} = N
Minimize \sum{2 * R * H} + \sum{R_m^2}
*/
#include <cmath>
#include <cstdio>
#include <iostream>

int n, m;
int ans = 1145141919;
int min_s[200005];
int min_v[200005];

int read(){
	int x = 0, f = 1; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
	return f ? x : -x;
}

int min(int a, int b){return a < b? a : b;}

void dfs(int dep, int V, int S, int R_pre, int H_pre){
	if(!dep){
		if(V == n) ans = min(ans, S);
		return;
	}
	if(S + min_s[dep] >= ans) return;
	if(V + min_v[dep] > n) return;
	if(2 * (n - V) / R_pre + S >= ans) return;
	for(int i = R_pre - 1; i >= dep; --i){
		if(dep == m) S = i * i; // 如果是最低层, 要加上底面积.
		int H_max = min(H_pre - 1, (n - min_v[dep-1] - V) / i / i);
		for(int j = H_max; j >= dep; --j){
			dfs(dep - 1, V + i * i * j, S + (i * j << 1), i, j);
		}
	}
}

int main(){
	n = read(), m = read();
	for(int i = 1; i <= m; ++i){
		min_s[i] = min_s[i-1] + (i * i << 1);
		min_v[i] = min_v[i-1] + (i * i * i);
	}
	dfs(m, 0, 0, sqrt(n) + 1, n + 1);
	printf("%d\n", ans == 1145141919? 0 : ans);
}

2. 击杀黄金蛋糕人马

题意简述

给定一个的长方形, 通过横着切或竖着切把它分为块, 在多种切法中, 肯定有让最大块的子长方形面积最小的切法, 求出这个最小面积.

数据范围:.

Solution

在看数据范围之前, 我就想到了一种时间复杂度非常优秀的做法: 二分最小面积, 看切出它的最小刀数是否小于.

一看的上界才, 谁还想去绞尽脑汁写 checker 呀,的记忆化搜索比二分好写太多了.

记 f[w][h][m]: 把的长方形切成块, 所有切分中最大块的最小面积.

然后, 思考怎么拆分子问题.

很容易想到, 可以枚举下刀的位置, 以及分为两大块后, 左右两块各应该再切成多少块.

边界情况:, 此时 f[w][h][m].

一共个状态, 每个状态会被考虑次, 时间复杂度, 虽然很劣, 但可通过此题.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>
#define INF 0x3f3f3f3f

int f[21][21][21];
int w, h, m;

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch);  ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
    return f ? x : -x;
}

int min(int a, int b){return a < b? a : b;}
int max(int a, int b){return a > b? a : b;}


int dfs(int w, int h, int m){
    if(m == 1) return w * h;
    if(w * h < m) return INF; // m 比面积还大, 不可能分成 m 块的.
    if(f[w][h][m]) return f[w][h][m];
    int res = INF;
    // 枚举横着切的点
    for(int i = 1; i < h; ++i){
        for(int k = 1; k < m; ++k){
            // 一刀分为上下两块, 再递归求解这两块的最大值
            int tmp = max(dfs(w, i, k), dfs(w, h - i, m - k));
            res = min(res, tmp);
        }
    }
    // 枚举竖着切的点
    for(int i = 1; i < w; ++i){
        for(int k = 1; k < m; ++k){
            // 一刀分为左右两块, 再递归求解这两块的最大值
            int tmp = max(dfs(i, h, k), dfs(w - i, h, m - k));
            res = min(res, tmp);
        }
    }
    return f[w][h][m] = res;
}

int main(){
    while(1){
        w = read(), h = read(), m = read();
        if(w == 0 and h == 0 and m == 0) break;
        memset(f, 0, sizeof(f));
        printf("%d\n", dfs(w, h, m));
    }
}

3. 寻找林克的回忆(1)

传送门 -- 洛谷 P1784 数独

题意简述

给定一个的数独, 给出一个可行解.

Solution

数独有行,列,个宫格, 分别用 row[r][d], col[c][d], block[b1][b2][d] 这三个 bool 数组来记录数字在第行、第列、第行第列宫格是否已被使用.

其中, 可用快速求出所在的宫格.

然后就是普通的 DFS 了.

时间复杂度最坏为为空格数, 但在所给约束条件下, 属于能过.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>

int n;

bool FLAG;

char map[10][10];
char in[10000];

bool row[10][12];
bool col[10][12];

bool block[3][3][12];

void dfs(int x, int y){
    if(FLAG) return;
    if(x == 9){
        FLAG = true;
        for(int i = 0; i < 9; ++i) std::cout << map[i] << std::endl;
        return;
    }
    if(y >= 9){dfs(x + 1, 0); return;} // 换行
    if(map[x][y] != '0'){dfs(x, y + 1); return;} // 跳过已经填过的点
    for(int d = 1; d <= 9; ++d){ // 枚举候选数字, 往下搜
        if(row[x][d] or col[y][d] or block[x/3][y/3][d]) continue;
        map[x][y] = d + '0';
        row[x][d] = col[y][d] = block[x/3][y/3][d] = true;
        dfs(x, y + 1);
        map[x][y] = '0';
        row[x][d] = col[y][d] = block[x/3][y/3][d] = false;
    }
}

int main(){
    //freopen("input.txt", "r", stdin);
    for(int i = 0; i < 9; ++i){
        std::cin >> map[i];
    }
    for(int i = 0; i < 9; ++i){
        for(int j = 0; j < 9; ++j){
            if(map[i][j] == '0') ++n;
            else row[i][map[i][j] xor 48] = col[j][map[i][j] xor 48] = block[i/3][j/3][map[i][j] xor 48] = true;
        }
    }
    dfs(0, 0);
}

4. 寻找林克的回忆(2)

传送门 -- 洛谷 P10481 Sudoku 传送门 -- 洛谷 P10482 Sudoku 2

题意简述

给定若干的数独, 分别给出一个可行解.

上一题的能过算法在这里是不能过.

Solution

爆搜代码过不了, 就需要找优化方法.

原来的爆搜代码, 是按从上到下, 从左到右的顺序依次填数.

假如是人来做数独, 人会怎么做?

我不知道别人是怎么做的, 反正我会先把所有能唯一确定的空先填上, 然后再找候选数最少的空进行尝试, 这样做是有道理的, 比起按顺序填数, 这种做法能够大大减少需要尝试的情况数.

这种搜索方式就是启发式搜索, 虽然最坏时间复杂度和原来一样, 但平均时间复杂度能减少到. 只要数据友好, 就能够通过.

为了高效找到候选数最少的空, 我们不再使用原来的 row, col, block 二维 bool 数组, 而是使用bitmask: 用二进制数描述每个数的使用情况.

具体来说, 就是用十位二进制数来描述某个数字是否被使用, 如果已被使用, 就把其对应位置为, 否则置为.

于是, 就可以用 row[i] 表示第行的使用情况, col[j] 表示第列的使用情况, block[b1][b2] 表示第行第列宫格的使用情况.

然后使用位运算高效完成这些基本操作:

(mask 是一个十位二进制数, d 是数字到)

操作对应位运算
数字是否被使用mask >> d & 1
标记为已被使用mask |= 1 << d
标记为未被使用mask &= ~(1 << d)
三个 masks 取并row[i] | col[j] | block[b1][b2]

显然, 行、列、宫格三个十位二进制数取并后得到的 mask, 就标志了该位置的数字使用情况,的数量就是候选数的数量, 可先用 __builtin_popcount 求出的数量, 再用来减得到的数量.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>

int n;
bool FLAG;

char map[10][10];
char in[10000];

int row[9], col[9];
int block[3][3];

int bitmask(int x, int y){
    return row[x] | col[y] | block[x/3][y/3];
}

void dfs(int step){
    if(FLAG) return;
    if(step == n){
        FLAG = true;
        for(int i = 0; i < 9; ++i) std::cout << map[i];
        std::cout << std::endl;
    }
    // 启发式, 找候选数最少的空
    int x = -1, y = -1, mini = 10;
    for(int i = 0; i < 9; ++i){
        for(int j = 0; j < 9; ++j){
            if(map[i][j] != '0') continue;
            int mask = bitmask(i, j);
            int cnt = 9 - __builtin_popcount(mask);
            if(cnt < mini) mini = cnt, x = i, y = j;
        }
    }
    int mask = bitmask(x, y);
    for(int d = 1; d <= 9; ++d){
        if(mask >> d & 1) continue; // 数字 d 已经被使用
        map[x][y] = d xor 48;
        row[x] |= 1 << d;
        col[y] |= 1 << d; 
        block[x/3][y/3] |= 1 << d; // 在该空填入 d

        dfs(step+1); // 继续搜

        map[x][y] = '0';
        row[x] &= ~(1 << d);
        col[y] &= ~(1 << d);
        block[x/3][y/3] &= ~(1 << d); // 回溯: 该空不填 d
    }
}

int main(){
//    freopen("input.txt", "r", stdin);
    std::ios::sync_with_stdio(false);
    while(std::cin >> in){
        if(strcmp(in, "end") == 0) return 0;
        FLAG = false; n = 0;
        memset(row, false, sizeof(row));
        memset(col, false, sizeof(col));
        memset(block, false, sizeof(block));
        for(int i = 0; i < 9; ++i){
            for(int j = 0; j < 9; ++j){
                map[i][j] = in[i*9 + j];
                if(map[i][j] == '.') map[i][j] = '0', ++n;
                else{
                    int d = map[i][j] xor 48;
                    row[i] |= 1 << d;
                    col[j] |= 1 << d;
                    block[i/3][j/3] |= 1 << d;
                }
            }
        }
        dfs(0);
    }
}

5. 寻找林克的回忆(4)

题意简述

给定若干的数独, 分别给出一个可行解.

上一题的能过算法在这里是不能过.

Solution

读完上题的 Solution 就可以发现, 我上一题在代码实现部分偷懒了, 我并未把所有能唯一确定的空先填上, 而只是找了候选数最少的空进行尝试, 每层搜索只填一个数, 自然不够高效.

换言之, 我们需要准确实现这个过程: 先把所有能唯一确定的空先填上, 然后再找候选数最少的空进行尝试.

需要注意的是, “能唯一确定的空” 是相对当前状态而言的, 如果上层搜索所作出的猜测不正确, 那么我们填入的这些 “能唯一确定的空” 就也需要回溯.

要如何优雅地实现 “启发式回溯” 呢?

很简单, 和普通的搜索回溯一样, 这里也是要 “撤销” 作出的操作, 唯一的区别就是操作可能不止一次, 自然想到用一个栈来记录所有填能唯一确定的空的操作, 并在开始填这些空时记录原来的操作栈的大小, 就可以在搜索失败后依次还原这些操作了.

Implementation:

#include <stack>
#include <cstdio>
#include <cstring>
#include <iostream>

int n;

char map[17][17];
char in[10000];

int row[17], col[17];
int block[4][4];

struct Record{
    int r, c, d;
};

std::stack<Record> stk;

int bitmask(int x, int y){
    return row[x] | col[y] | block[x/4][y/4];
}

void undo(int until){
    while(stk.size() > until){
        Record opt = stk.top(); stk.pop();
        map[opt.r][opt.c] = '-';
        row[opt.r] &= ~(1 << opt.d);
        col[opt.c] &= ~(1 << opt.d);
        block[opt.r/4][opt.c/4] &= ~(1 << opt.d);
    }
}

void make(int r, int c, int d){
    map[r][c] = 'A' - 1 + d;
    row[r] |= 1 << d;
    col[c] |= 1 << d;
    block[r/4][c/4] |= 1 << d;
    stk.push({r, c, d});
}

bool dfs(int step){
//    printf("step = %d\n", step);
    int stk_A = stk.size(); // 记录当前状态
    int step_A = step;
    // 填所有可唯一确定的数
    bool opted = true; // 是否有操作
    while(opted){
        opted = false;
        for(int i = 0; i < 16; ++i){
            for(int j = 0; j < 16; ++j){
                if(map[i][j] != '-') continue;
                int mask = bitmask(i, j);
                int cnt = 16 - __builtin_popcount(mask);
                if(cnt == 0){ // 没有可选的数, 矛盾!
                    undo(stk_A);
                    return false;
                }
                if(cnt == 1){
                    int d = __builtin_ctz(131070 & ~mask);
                    // 使用魔法找出唯一的数, 131070 = (1<<17)-2
                /*     等价写法
                    int d = 1;
                    while((mask >> d & 1)) ++d;
                */    
                    make(i, j, d); ++step; opted = true;
                }
            }
        }
    }
    // 填完了
    if(step == n){
        for(int i = 0; i < 16; ++i) std::cout << map[i] << std::endl;
        return true;
    }

    int stk_B = stk.size();
    int step_B = step;

    // 启发式, 找候选数最少的空
    int x = -1, y = -1, mini = 17;
    for(int i = 0; i < 16; ++i){
        for(int j = 0; j < 16; ++j){
            if(map[i][j] != '-') continue;
            int mask = bitmask(i, j);
            int cnt = 16 - __builtin_popcount(mask);
            if(cnt < mini) mini = cnt, x = i, y = j;
        }
    }

    int mask = bitmask(x, y);
    for(int d = 1; d <= 16; ++d){
        if(mask >> d & 1) continue;
        make(x, y, d); ++step;

        if(dfs(step)) return true; // 递归猜测

        undo(stk_B);
        step = step_B;
    }
    undo(stk_A); // 回溯 “可唯一确定的空”
    return false; // 这种情况无解
}

void solve(){
    n = 0;
    while(stk.size()) stk.pop();
    memset(row, 0, sizeof(row));
    memset(col, 0, sizeof(col));
    memset(block, 0, sizeof(block));
    for(int i = 0; i < 16; ++i){
        for(int j = 0; j < 16; ++j){
            if(map[i][j] == '-') ++n;
            else{
                int d = map[i][j] - 'A' + 1;
                row[i] |= 1 << d;
                col[j] |= 1 << d;
                block[i/4][j/4] |= 1 << d;
            }
        }
    }
    dfs(0);
}

int main(){
//    freopen("in.txt", "r", stdin);
    std::cin.sync_with_stdio(false);
    int i = 0;
    while(std::cin >> in){
        strcpy(map[i++], in);
        if(i == 16){solve(); i = 0;}
    }
}

但, 还没有结束.

这份代码 TLE 了.

最令我伤心的是, 我花了一个晚上 Debug 它 (虽然好像没bug), 最后才发现是因为剪枝还不够强 (sad).

在这份代码上花了太多时间, 所以尽管它没能 AC , 我还是要把它贴出来.

那么这份代码为什么无法通过呢?

因为, 我只考虑了考虑了一个空只能填一个字母的情况, 没考虑一个字母只能填在某个空的情况.

比如, 在某一行中, 有个空可以填 C 和 F, 其它空都有别的可填字母, 唯独没有 F, 此时 F 就只能填在这个空.

这是个非常强力的剪枝, 也是现实数独中常用的解题技巧, 但我在写代码时却没考虑到.

修改后的代码如下:

bool dfs(int filled){

    int now = stk.size(); // 记录当前状态

    bool opted = true; // 是否有操作
    while(opted){
        opted = false;
        // 只有 1 个候选数的空
        for(int i = 0; i < 16; ++i){
            for(int j = 0; j < 16; ++j){
                if(map[i][j] != '-') continue;
                int mask = bitmask(i, j);
                int cnt = 16 - __builtin_popcount(mask);
                if(cnt == 1){
                    int d = __builtin_ctz(131070 & ~mask);  
                    make(i, j, d); ++filled; opted = true;
                }
            }
        }
        // 只可填在 1 个空的字母
            // 检查每一行
        for(int r = 0; r < 16; ++r){
            for(int d = 1; d <= 16; ++d){
                if(row[r] >> d & 1) continue; // 用过了, 跳过
                int place = 0;
                int last = -1;
                for(int c = 0; c < 16; ++c){
                    int mask = bitmask(r, c);
                    if(map[r][c] != '-' or mask >> d & 1) continue;
                    ++place, last = c;
                }
                if(place == 1){ // 只出现 1 次
                    make(r, last, d); ++filled; opted = true;
                }
            }
        }
            // 检查每一列
        for(int c = 0; c < 16; ++c){
            for(int d = 1; d <= 16; ++d){
                if(col[c] >> d & 1) continue; // 用过了, 跳过
                int place = 0;
                int last = -1;
                for(int r = 0; r < 16; ++r){
                    int mask = bitmask(r, c);
                    if(map[r][c] != '-' or mask >> d & 1) continue;
                    ++place, last = r;
                }
                if(place == 1){ // 只出现 1 次                    
                    make(last, c, d); ++filled; opted = true;
                }
            }
        }
            // 检查每一个宫
        for(int b1 = 0; b1 < 4; ++b1){
            for(int b2 = 0; b2 < 4; ++b2){
                for(int d = 1; d <= 16; ++d){
                    if(block[b1][b2] >> d & 1) continue;
                    int place = 0;
                    int last = -1;
                    for(int r_offset = 0; r_offset < 4; ++r_offset){
                        for(int c_offset = 0; c_offset < 4; ++c_offset){
                            int r = b1 * 4 + r_offset;
                            int c = b2 * 4 + c_offset;
                            int mask = bitmask(r, c);
                            if(map[r][c] != '-' or mask >> d & 1) continue;
                            ++place, last = (r << 4) | c;
                        }
                    }
                    if(place == 1){ // 只出现 1 次
                        int r = last >> 4, c = last & 15;
                        make(r, c, d); ++filled; opted = true;
                    }
                }
            }
        }
                // 如果上面的操作导致矛盾, 就撤回
        for(int i = 0; i < 16; ++i){
            for(int j = 0; j < 16; ++j){
                if(map[i][j] != '-') continue;
                int mask = bitmask(i, j);
                int cnt = 16 - __builtin_popcount(mask);
                if(cnt == 0){
                    undo(now);
                    return false;
                }
            }
        }
        // 如果上面的操作导致矛盾, 就撤回
        for(int i = 0; i < 16; ++i){
            for(int j = 0; j < 16; ++j){
                if(map[i][j] != '-') continue;
                int mask = bitmask(i, j);
                if(__builtin_popcount(mask) == 16){
                    undo(now);
                    return false;
                }
            }
        }
    }
    // 填完了
    if(filled == n){
        for(int i = 0; i < 16; ++i) std::cout << map[i] << std::endl;
        return true;
    }

    // 启发式, 找候选数最少的空
    int x = -1, y = -1, mini = 17;
    for(int i = 0; i < 16; ++i){
        for(int j = 0; j < 16; ++j){
            if(map[i][j] != '-') continue;
            int mask = bitmask(i, j);
            int cnt = 16 - __builtin_popcount(mask);
            if(cnt < mini) mini = cnt, x = i, y = j;
        }
    }

    int _now_ = stk.size();
    int mask = bitmask(x, y);
    for(int d = 1; d <= 16; ++d){
        if(mask >> d & 1) continue;
        make(x, y, d);
        if(dfs(filled+1)) return true; // 递归猜测
        undo(_now_);
    }
    undo(now); // 回溯 “可唯一确定的空”
    return false; // 这种情况无解
}

这份代码只得了分, 有一个测试点 T 飞了.

啊? 这都过不了?

冷静思考了一下, 用层 for 循环去找只可填在 1 个空的字母 , 效率肯定低 (但我真的以为这个常数可以忽略不计呀呜呜). 需要更极致的优化.

稍微动一下脑筋, 其实我们可以用两个掩码 once 和 twice 分别记录出现某一单元 至少出现次和至少出现次的候选数, 遍历单元格的时候, 对于当前格子的候选数掩码, 先更新 twice |= (once & s), 再更新 once |= s, 遍历结束后, once & ~twice 就是只出现次的候选数了.

利用这个trick可以减少一重循环 .

于是这个优化到可能只有正在写这篇题解时的我才能看懂的最终版本它来了:

bool dfs(int filled){

    int now = stk.size(); // 记录当前状态

    bool opted = true; // 是否有操作
    while(opted){
        opted = false;
        // 只有 1 个候选数的空
        for(int i = 0; i < 16; ++i){
            for(int j = 0; j < 16; ++j){
                if(map[i][j] != '-') continue;
                int mask = bitmask(i, j);
                int cnt = 16 - __builtin_popcount(mask);
                if(cnt == 1){
                    int d = __builtin_ctz(131070 & ~mask);  
                    make(i, j, d); ++filled; opted = true;
                }
            }
        }
        // 只可填在 1 个空的字母
            // 检查每一行
        for(int r = 0; r < 16; ++r){
            int once = 0, twice = 0;
            int candidates[16];
            for(int c = 0; c < 16; ++c){
                if(map[r][c] != '-') continue;
                candidates[c] = ~bitmask(r, c) & 131070;
                twice |= (once & candidates[c]); once |= candidates[c];
            }
            int cats = once & ~twice;
            if(cats){
                for(int c = 0; c < 16; ++c){
                    if(map[r][c] != '-') continue;
                    int single = cats & candidates[c];
                    if(single){
                        int d = __builtin_ctz(single);
                        make(r, c, d); ++filled; opted = true;
                    }
                }
            }
        }
            // 检查每一列
        for(int c = 0; c < 16; ++c){
            int once = 0, twice = 0;
            int candidates[16];
            for(int r = 0; r < 16; ++r){
                if(map[r][c] != '-') continue;
                candidates[r] = ~bitmask(r, c) & 131070;
                twice |= (once & candidates[r]); once |= candidates[r];
            }
            int cats = once & ~twice;
            if(cats){
                for(int r = 0; r < 16; ++r){
                    if(map[r][c] != '-') continue;
                    int single = cats & candidates[r];
                    if(single){
                        int d = __builtin_ctz(single);
                        make(r, c, d); ++filled; opted = true;
                    }
                }
            }
        }
            // 检查每一个宫
        for(int b1 = 0; b1 < 4; ++b1){
            for(int b2 = 0; b2 < 4; ++b2){
                int once = 0, twice = 0;
                int candidates[16];
                for(int i = 0; i < 16; ++i) {
                    int r = (b1 << 2) | (i >> 2);
                    int c = (b2 << 2) | (i & 3);
                    if(map[r][c] == '-') {
                        candidates[i] = ~bitmask(r,c) & 131070;
                        twice |= (once & candidates[i]);
                        once |= candidates[i];
                    }
                }
                int cats = once & ~twice;
                if(cats){
                    for(int i = 0; i < 16; ++i){
                        int r = (b1 << 2) | (i >> 2);
                        int c = (b2 << 2) | (i & 3);
                        if(map[r][c] == '-') {
                            int single = cats & candidates[i];
                            if(single){
                                int d = __builtin_ctz(single);
                                make(r, c, d); ++filled; opted = true;
                            }
                        }
                    }
                }
            }
        }

        // 如果上面的操作导致矛盾, 就撤回
        for(int i = 0; i < 16; ++i){
            for(int j = 0; j < 16; ++j){
                if(map[i][j] != '-') continue;
                int mask = bitmask(i, j);
                if(__builtin_popcount(mask) == 16){
                    undo(now);
                    return false;
                }
            }
        }
    }
    // 填完了
    if(filled == n){
        for(int i = 0; i < 16; ++i) std::cout << map[i] << std::endl;
        return true;
    }

    // 启发式, 找候选数最少的空
    int x = -1, y = -1, mini = 17;
    for(int i = 0; i < 16; ++i){
        for(int j = 0; j < 16; ++j){
            if(map[i][j] != '-') continue;
            int mask = bitmask(i, j);
            int cnt = 16 - __builtin_popcount(mask);
            if(cnt < mini) mini = cnt, x = i, y = j;
        }
    }

    int _now_ = stk.size();
    int mask = bitmask(x, y);
    for(int d = 1; d <= 16; ++d){
        if(mask >> d & 1) continue;
        make(x, y, d);
        if(dfs(filled+1)) return true; // 递归猜测
        undo(_now_);
    }
    undo(now); // 回溯 “可唯一确定的空”
    return false; // 这种情况无解
}

折腾了一个晚上, 最终才以ms 的时间通过此题.

评测记录

还是太菜了呜呜呜.

6. 寻找林克的回忆(4) [DLX]

题意简述

同 5. 寻找林克的回忆(4)

但题目名称引导使用 Dancing Links X Algorithm.

前置知识: Dancing Links.

Solution

这里默认读者已经会用 DLX 求解 01 精确覆盖问题 . 相关内容我已在博客的另一篇文章详细介绍, 这里不做赘述.

首要问题是把数独问题转化为 01 精确覆盖问题.

用三元组表示数独的第行, 第列, 填入的是数字, 这个条件等价于以下条约束:

  1. 行-数字约束: 第行必须有数字.
  2. 列-数字约束: 第列必须有数字.
  3. 宫-数字约束:所在宫必须有数字.
  4. 唯一性约束: 格子只能填一个数.

又因为取遍~这个数, 很容易知道上面这条约束分别有个, 因此总共就是个约束.

又因为这个三元组就代表了一个选择, 一共可以有个不同的三元组, 也就是说有个选择.

于是,数独问题所对应的 01 精确覆盖问题 , 就可以转化为行,列的 Dancing Links进行求解.

具体应该怎么进行呢?

在读入之前, 先插入所有的对, 代表所有选择.

然后, 在读入时, 把读入的已填充位置视为 “强制选择”, 也就是在个选择中必须选择, 而一次选择就是一次dance, 我们需要划掉所有和有矛盾的选择.

最后, 再调用dance函数进行搜索求解.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>

const int MAX_C = 16 * 16 * 4;
const int MAX_R = 16 * 16 * 16;
const int SIZE = MAX_C + MAX_R * 4 + 10;
int stack[SIZE];

char in[20];
char map[17][17];
char ans[17][17];

int read(){
	int x = 0, f = 1; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
	return f ? x : -x;
}

struct DLX{
	int n, m, tot; // n * m的大小, tot是元素索引 
	int first[MAX_R + 10], size[MAX_C + 10];
	int up[SIZE], down[SIZE], left[SIZE], right[SIZE];
	int col[SIZE], raw[SIZE];
	bool FLAG;
	
	void build(const int &r, const int &c){
		n = r, m = c;
		for(int i = 0; i <= c; ++i){ // 1行, c列, 0是指示 
			left[i] = i - 1, right[i] = i + 1;
			up[i] = down[i] = i;
		}
		left[0] = c, right[c] = 0;
		FLAG = false;
		tot = c; // 漏了这行直接爆炸
		memset(size, 0, sizeof(size));
		memset(first, 0, sizeof(first)); 
	}
	
	void remove(const int &c){ // 删除第 c 列 
		right[left[c]] = right[c], left[right[c]] = left[c];
		for(int i = down[c]; i != c; i = down[i]){ // 往下移动, 枚举 c 的每个元素 i, 删除 i 所在行. 因为是环状链表, 最后会绕回 c 
			for(int j = right[i]; j != i; j = right[j]){ // 往右移动, 因为是环状链表, 最后会绕回 i
				down[up[j]] = down[j], up[down[j]] = up[j];
				--size[col[j]]; // 别忘了减掉列大小 
			}
		}  
	}
	
	void recover(const int &c){ // 恢复第 c 列, 与 remove 操作完全相反 
		for(int i = up[c]; i != c; i = up[i]){
			for(int j = left[i]; j != i; j = left[j]){
				down[up[j]] = up[down[j]] = j, ++size[col[j]];
			}
		}
		right[left[c]] = left[right[c]] = c;
	} 
	
	void insert(const int &r, const int &c){
        raw[++tot] = r, col[tot] = c, ++size[c];
        down[tot] = down[c], up[tot] = c;
        up[down[c]] = tot, down[c] = tot;
        if(!first[r]) first[r] = left[tot] = right[tot] = tot;
        else{
            left[tot] = first[r];
            right[tot] = right[first[r]];

            left[right[first[r]]] = tot;
            right[first[r]] = tot;
        }
    }
    void dance(int step){
		if(FLAG) return;
        if(!right[0]){
			// 复制原有解
			for(int i = 0; i < 16; ++i) for(int j = 0; j < 16; ++j) ans[i][j] = map[i][j];
            // 转换为答案
			for(int i = 0; i < step; ++i){
				const int r = stack[i] >> 8;
				const int c = (stack[i] & 0xff) >> 4; 
				const int d = stack[i] & 0xf;
				ans[r][c] = 'A' + d;
			}
			FLAG = true; return;
        }
        int c = right[0];
        for(int i = right[0]; i; i = right[i]) if(size[i] < size[c]) c = i;
        remove(c);
        for(int i = down[c]; i != c; i = down[i]){
            stack[step] = raw[i];
            for(int j = right[i]; j != i; j = right[j]) remove(col[j]);
            dance(step+1); if(FLAG) return;
            for(int j = left[i]; j != i; j = left[j]) recover(col[j]);
        } 
        recover(c);
    }
}solver;

void Insert(int x, int y, int z){
	// (x, y, z) 映射为一维(行)
	int r = (x << 8) | (y << 4) | z; 
	
	// 行-数字约束: 第 x 行必须有数字 z, 把 (行, 数字) 映射到 [1, 256]
	solver.insert(r, x * 16 + z + 1);
	// 列-数字约束: 第 y 列必须有数字 z, 把 (列, 数字) 映射到 (256, 512]
	solver.insert(r, y * 16 + z + 256 + 1);
	// 宫格-数字约束: (x, y) 所在的宫格必须有数字 z.
	// 这个宫格的坐标是 (x / 4, y / 4), 映射为一维就是 (x / 4) * 4 + (y / 4)
	const int block = (x / 4) * 4 + (y / 4);
	// 那么, ([x / 4, y / 4], z) 就映射到 (512, 768]
	solver.insert(r, block * 16 + z + 512 + 1);
	// 格子只能填一次约束, 映射到 (768, 1024]
	solver.insert(r, x * 16 + y + 768 + 1);
}

void solve(){
	solver.build(MAX_R, MAX_C);
	// 全空约束, 即插入所有可能性
	for(int i = 0; i < 16; ++i){
		for(int j = 0; j < 16; ++j){
			for(int d = 0; d < 16; ++d){
				Insert(i, j, d);
			}
		}
	}
	// 硬性约
	for(int i = 0; i < 16; ++i){
		for(int j = 0; j < 16; ++j){
			if(map[i][j] != '-'){ // 强制选择这一行, 也就是进行一次 dance
				const int d = map[i][j] - 'A';
				const int r = (i << 8) | (j << 4) | d;

				const int c1 = i * 16 + d + 1;
				
				int target = -1;
				for(int k = solver.down[c1]; k != c1; k = solver.down[k]){
					if(solver.raw[k] == r){target = k; break;}
				}
				if(target == -1) continue;
				solver.remove(c1);
				for(int k = solver.right[target]; k != target; k = solver.right[k])
					solver.remove(solver.col[k]);
			}
		}
	}
	solver.dance(0);
	for(int i = 0; i < 16; ++i) std::cout << ans[i] << std::endl;
}

int main(){
//	freopen("input.txt", "r", stdin);
	int i = 0;
	while(std::cin >> in){
		strcpy(map[i++], in);
		if(i == 16){solve(); i = 0;}
	}
}

这份代码比上一题的 DFS 快, 只用了ms.

7. 寻找林克的回忆(3)

传送门 -- 洛谷 P1074 [NOIP 2009 提高组] 靶形数独

题意简述

给定一个的数独, 每个格子有不同的得分:

  • 正中心的格子为分.
  • 最外面一圈的格子为分, 从中间往外面每圈的格子分数依次递减.

示意图:

靶形数独

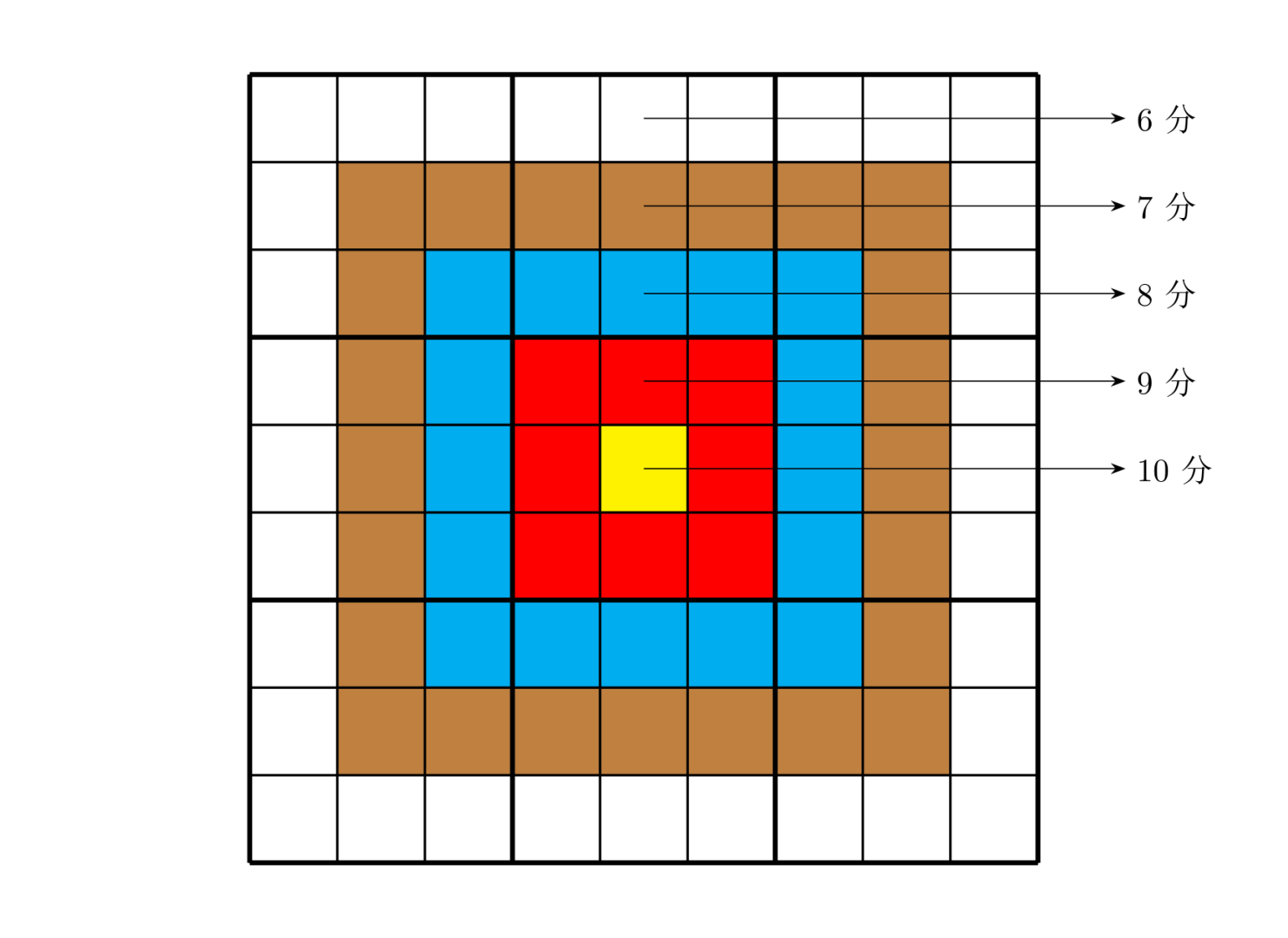
总分值为每个方格的分值和填在格子中的数字的乘积之和, 即格子分值填入的数字, 试求出最大得分.

Solution

使用目前最快的 DLX 算法来求解数独, 每得到一组可行解就更新最大得分即可.

抄抄板就行, 唯一的改动只有 dance 函数中对 right[0] == 0 的处理.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>
#define N 9

const int MAX_C = N * N * 4;
const int MAX_R = N * N * N;
const int SIZE = MAX_C + MAX_R * 4 + 10;
int stack[SIZE];

int map[N+1][N+1];
int sol[N+1][N+1];
long long ans = -1;

int read(){
	int x = 0, f = 1; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
	return f ? x : -x;
}

int sqrt(int x){
    if(x == 1) return 1;
    if(x == 4) return 2;
    if(x == 9) return 3;
    if(x == 16) return 4;
    if(x == 25) return 5;
    return 114514;
}

int get_score(int r, int c, int d){
    if(r == 0 || r == N-1 || c == 0 || c == N-1) return d * 6;
    if(r == 1 || r == N-2 || c == 1 || c == N-2) return d * 7;
    if(r == 2 || r == N-3 || c == 2 || c == N-3) return d * 8;
    if(r == 3 || r == N-4 || c == 3 || c == N-4) return d * 9;
    if(r == 4 || r == N-5 || c == 4 || c == N-5) return d * 10;
    return 0;
}

struct DLX{
	int n, m, tot; // n * m的大小, tot是元素索引 
	int first[MAX_R + 10], size[MAX_C + 10];
	int up[SIZE], down[SIZE], left[SIZE], right[SIZE];
	int col[SIZE], raw[SIZE];
	
	void build(const int &r, const int &c){
		n = r, m = c;
		for(int i = 0; i <= c; ++i){ // 1行, c列, 0是指示 
			left[i] = i - 1, right[i] = i + 1;
			up[i] = down[i] = i;
		}
		left[0] = c, right[c] = 0;
		tot = c; // 漏了这行直接爆炸
		memset(size, 0, sizeof(size));
		memset(first, 0, sizeof(first)); 
	}
	
	void remove(const int &c){ // 删除第 c 列 
		right[left[c]] = right[c], left[right[c]] = left[c];
		for(int i = down[c]; i != c; i = down[i]){ // 往下移动, 枚举 c 的每个元素 i, 删除 i 所在行. 因为是环状链表, 最后会绕回 c 
			for(int j = right[i]; j != i; j = right[j]){ // 往右移动, 因为是环状链表, 最后会绕回 i
				down[up[j]] = down[j], up[down[j]] = up[j];
				--size[col[j]]; // 别忘了减掉列大小 
			}
		}  
	}
	
	void recover(const int &c){ // 恢复第 c 列, 与 remove 操作完全相反 
		for(int i = up[c]; i != c; i = up[i]){
			for(int j = left[i]; j != i; j = left[j]){
				down[up[j]] = up[down[j]] = j, ++size[col[j]];
			}
		}
		right[left[c]] = left[right[c]] = c;
	} 
	
	void insert(const int &r, const int &c){
        raw[++tot] = r, col[tot] = c, ++size[c];
        down[tot] = down[c], up[tot] = c;
        up[down[c]] = tot, down[c] = tot;
        if(!first[r]) first[r] = left[tot] = right[tot] = tot;
        else{
            left[tot] = first[r];
            right[tot] = right[first[r]];

            left[right[first[r]]] = tot;
            right[first[r]] = tot;
        }
    }
    void dance(int step){
        if(!right[0]){
			// 复制原有解
			for(int i = 0; i < N; ++i) for(int j = 0; j < N; ++j) sol[i][j] = map[i][j];
            // 转换为答案
			for(int i = 0; i < step; ++i){
				const int val = stack[i];
                const int r = val / (N * N);
                const int c = (val / N) % N;
                const int d = val % N;
                sol[r][c] = d + 1;
			}
            long long res = 0;
            for(int i = 0; i < N; ++i) for(int j = 0; j < N; ++j)
                res += get_score(i, j, sol[i][j]);
		    ans = std::max(ans, res);
            return;
        }
        int c = right[0];
        for(int i = right[0]; i; i = right[i]) if(size[i] < size[c]) c = i;
        remove(c);
        for(int i = down[c]; i != c; i = down[i]){
            stack[step] = raw[i];
            for(int j = right[i]; j != i; j = right[j]) remove(col[j]);
            dance(step+1);
            for(int j = left[i]; j != i; j = left[j]) recover(col[j]);
        } 
        recover(c);
    }
}solver;

void Insert(int x, int y, int z){

    int r = x * N * N + y * N + z;

	solver.insert(r, x * N + z + 1);
	solver.insert(r, y * N + z + N * N + 1);
	const int block_size = sqrt(N);
    const int block = (x / block_size) * block_size + (y / block_size);
	solver.insert(r, block * N + z + N * N * 2 + 1);
	solver.insert(r, x * N + y + N * N * 3 + 1);
}

void solve(){
	solver.build(MAX_R, MAX_C);
	for(int i = 0; i < N; ++i){
		for(int j = 0; j < N; ++j){
			for(int d = 0; d < N; ++d){
				Insert(i, j, d);
			}
		}
	}
	for(int i = 0; i < N; ++i){
		for(int j = 0; j < N; ++j){
			if(map[i][j]){
				int d = map[i][j] - 1;
                const int r = i * N * N + j * N + d;
				const int c1 = i * N + d + 1;
				
				int target = -1;
				for(int k = solver.down[c1]; k != c1; k = solver.down[k]){
					if(solver.raw[k] == r){target = k; break;}
				}
				if(target == -1) continue;
				solver.remove(c1);
				for(int k = solver.right[target]; k != target; k = solver.right[k])
					solver.remove(solver.col[k]);
			}
		}
	}
	solver.dance(0);
	printf("%lld\n", ans);
}

int main(){
//	freopen("in.txt", "r", stdin);
    std::ios::sync_with_stdio(false);
	for(int i = 0; i < 9; ++i){
        for(int j = 0; j < 9; ++j){
            std::cin >> map[i][j];
        }
    }
    solve();
}

8. 滚石柱

传送门

题意简述

不知道怎么简述, 所以我直接把题目搬过来了:

C06

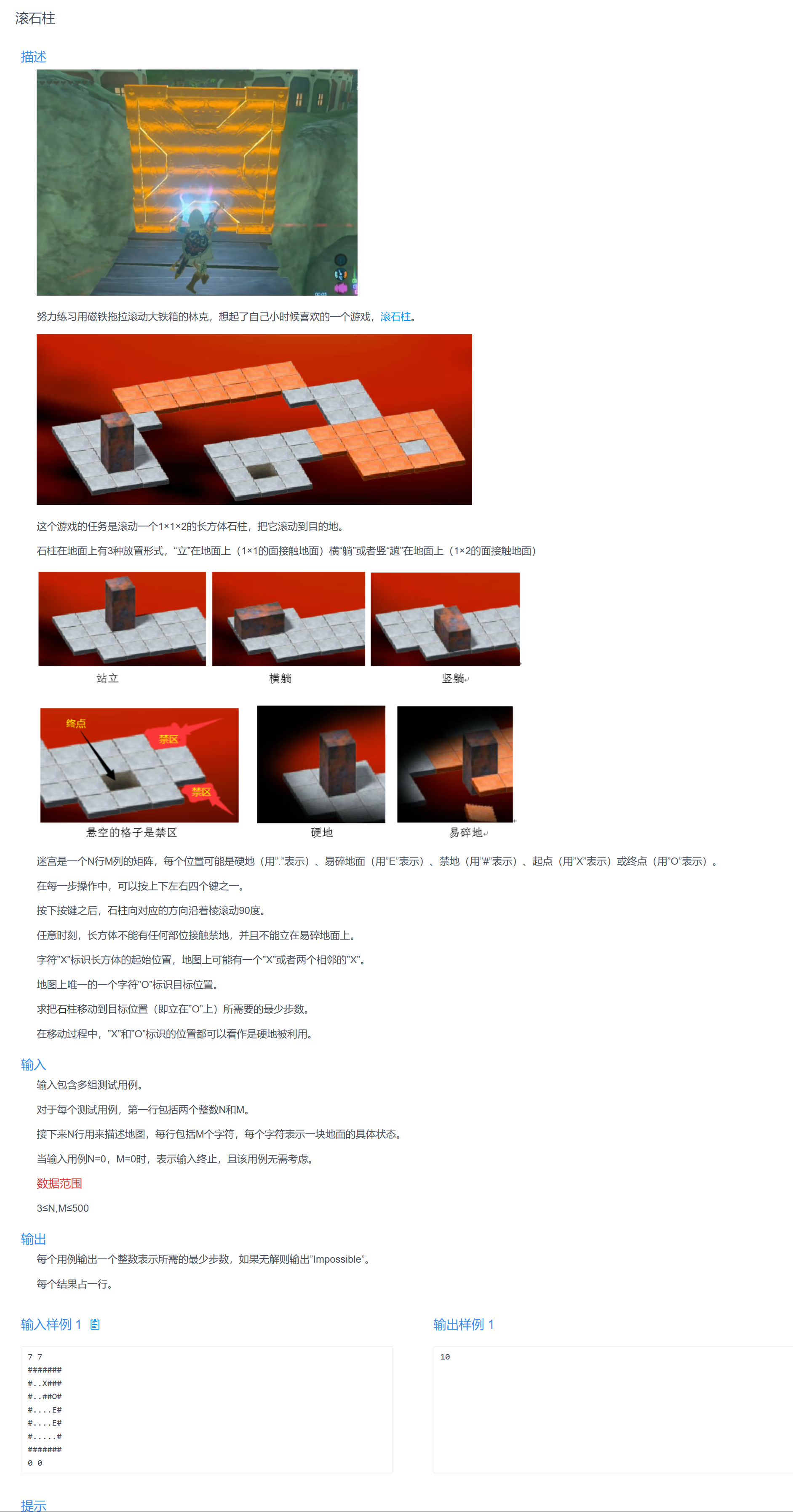
Solution

没啥思维难度, 如果像我一样是用石柱放置形式 + 一个坐标来描述石柱位置的话, 在翻转时要正确处理好下一个坐标 .

需要分好几种情况进行讨论, 代码相对繁琐.

AC Code:

#include <queue>
#include <cstdio>
#include <iostream>
#include <unordered_map>

int n, m, o1, o2;
char map[505][505];

enum State{TANG_H, TANG_V, LI};

struct Stone{
    State state;
    int x, y;
    // 如果是LI, (x, y) 表示触底点坐标
    // 如果是TANG_H, (x, y) 表示左边点坐标
    // 如果是TANG_V, (x, y) 表示上边点坐标
    long long to_ll(){
        return (long long)state * 1145141919LL + x * 501 + y;
    }
}stone;

std::unordered_map<long long, bool> vis;

void bfs(){
    vis.clear();
    std::queue<std::pair<Stone, int>> q;
    q.push({stone, 0});
    vis[stone.to_ll()] = true;
    while(q.size()){
        Stone s = q.front().first;
        int step = q.front().second;
        q.pop();
        if(s.x == o1 and s.y == o2 and s.state == LI){
            printf("%d\n", step);
            return;
        }
        if(s.state == LI){
            // 上
            if(s.x > 1 and map[s.x - 1][s.y] != '#' and map[s.x - 2][s.y] != '#'){
                Stone tmp = s; tmp.x -= 2; tmp.state = TANG_V;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 下
            if(s.x < n - 2 and map[s.x + 1][s.y] != '#' and map[s.x + 2][s.y] != '#'){
                Stone tmp = s; ++tmp.x; tmp.state = TANG_V;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 左
            if(s.y > 1 and map[s.x][s.y - 1] != '#' and map[s.x][s.y - 2] != '#'){
                Stone tmp = s; tmp.y -= 2; tmp.state = TANG_H;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 右
            if(s.y < m - 2 and map[s.x][s.y + 1] != '#' and map[s.x][s.y + 2] != '#'){
                Stone tmp = s; ++tmp.y; tmp.state = TANG_H;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
        }
        else if(s.state == TANG_H){
            // 上
            if(s.x > 0 and map[s.x - 1][s.y] != '#' and map[s.x - 1][s.y + 1] != '#'){
                Stone tmp = s; --tmp.x;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 下
            if(s.x < n - 1 and map[s.x + 1][s.y] != '#' and map[s.x + 1][s.y + 1] != '#'){
                Stone tmp = s; ++tmp.x;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 左
            if(s.y > 0 and map[s.x][s.y - 1] != '#' and map[s.x][s.y - 1] != 'E'){
                Stone tmp = s; --tmp.y; tmp.state = LI;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 右
            if(s.y < m - 2 and map[s.x][s.y + 2] != '#' and map[s.x][s.y + 2] != 'E'){
                Stone tmp = s; tmp.y += 2; tmp.state = LI;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
        }
        else if(s.state == TANG_V){
            // 左
            if(s.y > 0 and map[s.x][s.y - 1] != '#' and map[s.x + 1][s.y - 1] != '#'){
                Stone tmp = s; --tmp.y;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 右
            if(s.y < m - 1 and map[s.x][s.y + 1] != '#' and map[s.x + 1][s.y + 1] != '#'){
                Stone tmp = s; ++tmp.y;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 上
            if(s.x > 0 and map[s.x - 1][s.y] != '#' and map[s.x - 1][s.y] != 'E'){
                Stone tmp = s; --tmp.x; tmp.state = LI;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
            // 下
            if(s.x < n - 2 and map[s.x + 2][s.y] != '#' and map[s.x + 2][s.y] != 'E'){
                Stone tmp = s; tmp.x += 2; tmp.state = LI;
                if(!vis[tmp.to_ll()]) q.push({tmp, step + 1}), vis[tmp.to_ll()] = true;
            }
        }
    }
    printf("Impossible\n");
}

int main(){
//    freopen("in.txt", "r", stdin);
    while(~scanf("%d%d", &n, &m) and n and m){
        stone.x = stone.y = -1;
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < m; ++j){
                char ch = ' ';
                while(ch == ' ' or ch == '\n') ch = getchar();
                map[i][j] = ch;
                if(ch == 'O') o1 = i, o2 = j;
                if(ch == 'X'){
                    if(stone.x == -1) stone.x = i, stone.y = j, stone.state = LI;
                    else{
                        if(stone.x == i - 1 or stone.x == i + 1) stone.state = TANG_V;
                        else stone.state = TANG_H;
                    }
                }
            }
        }
        bfs();
    }
}

9. 维修电路

传送门 -- 洛谷 P4667

题意简述

简述不了, 进传送门看题吧.

Solution

解决此类问题的基本思想在我的博客中已有记载.

不要被洛谷的神秘标签带偏了, 这只是01 BFS.

tags.png

从一个格子沿对角线可以走到其它个格子, 其中有种走法不需要转动电线,种走法需要转动电线. (假设这个格子不在边界上)

我们知道, BFS的层序遍历特点能保证终点第一次被访问时就是最优解, 但如果我们在遍历时同时把这种走法都放进队首拓展, 就会破坏这样的最优解性质, 因为先被访问的点不一定有最少的转动电线次数.

为了维护BFS的最优解性质, 我们每次:

  • 把不需要转动电线的走法放到队首.
  • 把需要转动电线的走法放到队尾.

再取队首拓展, 就能保证每次拓展的点都是最优解.

然后要注意格点和格子的坐标关系, 这个自己画图就懂了, 我不做赘述.

已在代码里附上错误的 DFS 代码, 可思考为什么这种 DFS 写法是错误的.

AC Code:

#include <deque>
#include <cstdio>
#include <cstring>
#include <iostream>

int T;
int n, m;
char map[505][505];
int f[505][505];

void dfs(int x, int y, int step){
        if(step >= f[x][y] or step > n + m) return;
        f[x][y] = step;
        if(x > 0 and y > 0 and map[x][y] != '/') dfs(x-1, y-1, step);
        if(x < n and y < m and map[x+1][y+1] != '/') dfs(x+1, y+1, step);
        if(x > 0 and y < m and map[x][y+1] == '/') dfs(x-1, y+1, step);
        if(x < n and y > 0 and map[x+1][y] == '/') dfs(x+1, y-1, step);

        if(x > 0 and y > 0 and map[x][y] == '/') dfs(x-1, y-1, step+1);
        if(x < n and y < m and map[x+1][y+1] == '/') dfs(x+1, y+1, step+1);
        if(x > 0 and y < m and map[x][y+1] != '/') dfs(x-1, y+1, step+1);
        if(x < n and y > 0 and map[x+1][y] != '/') dfs(x+1, y-1, step+1);
}

struct State{
    int x, y, step;
};

bool bfs(){
    std::deque<State> q;
    q.push_front({0, 0});
    while(q.size()){
        State cur = q.front(); q.pop_front();
        if(cur.x == n and cur.y == m){
            printf("%d\n", cur.step);
            return true;
        }
        f[cur.x][cur.y] = 0;
        if(cur.x > 0 and cur.y > 0 and map[cur.x][cur.y] != '/' and f[cur.x-1][cur.y-1]) q.push_front({cur.x-1, cur.y-1, cur.step});
        if(cur.x < n and cur.y < m and map[cur.x+1][cur.y+1] != '/' and f[cur.x+1][cur.y+1]) q.push_front({cur.x+1, cur.y+1, cur.step});
        if(cur.x > 0 and cur.y < m and map[cur.x][cur.y+1] == '/' and f[cur.x-1][cur.y+1]) q.push_front({cur.x-1, cur.y+1, cur.step});
        if(cur.x < n and cur.y > 0 and map[cur.x+1][cur.y] == '/' and f[cur.x+1][cur.y-1]) q.push_front({cur.x+1, cur.y-1, cur.step});

        if(cur.x > 0 and cur.y > 0 and map[cur.x][cur.y] == '/' and f[cur.x-1][cur.y-1]) q.push_back({cur.x-1, cur.y-1, cur.step+1});
        if(cur.x < n and cur.y < m and map[cur.x+1][cur.y+1] == '/' and f[cur.x+1][cur.y+1]) q.push_back({cur.x+1, cur.y+1, cur.step+1});
        if(cur.x > 0 and cur.y < m and map[cur.x][cur.y+1] != '/' and f[cur.x-1][cur.y+1]) q.push_back({cur.x-1, cur.y+1, cur.step+1});
        if(cur.x < n and cur.y > 0 and map[cur.x+1][cur.y] != '/' and f[cur.x+1][cur.y-1]) q.push_back({cur.x+1, cur.y-1, cur.step+1});
    }
    return false;
}

void solve(){
    std::cin >> n >> m;
    for(int i = 1; i <= n; ++i){
        for(int j = 1; j <= m; ++j){
            char ch = ' ';
            while(ch != '\\' and ch != '/') ch = getchar();
            map[i][j] = ch;
        }
    }
    memset(f, 0x3f, sizeof(f));
    if(!bfs()) puts("NO SOLUTION");
}

int main(){
//    freopen("in.txt", "r", stdin);
    std::cin >> T;
    while(T--) solve();
}

10. 最省赛程

题意简述

有个城市,条双向道路, 第座城市的单位油价为, 通过第条道路需消耗的油.

回答个询问, 每个询问会给出三个数,,, 分别表示油箱容量, 起点城市编号, 终点城市编号.

初始油箱为空, 求从起点到终点所需最小花费.

若无法到达终点, 输出 impossible .

数据范围:

Solution

既有油量又有价格, 似乎是个二元问题.

考虑状态, 其中表示当前城市,表示当前油量,表示抵达当前城市的花费. 显然, 对相同的城市和相同的, 我们会想要最小化.

而状态可以由这两条路径进行转移:

  • 在该城市加单位的油, 状态变成.
  • 选择走油耗为的道路前往城市, 状态变成.

相比于普通的 Dijkstra, 我们只需要把原来表示距离的数组 dis[N] 拓展为二维 dis[C][N] 即可.

也可以换一种角度理解: 把每个点拆成个点, 除了可以在城市与城市之间走, 也可以花费从走到.

单次询问的时间复杂度为.

如果所有输入都取到上界的话, 应该是过不了的, 不过我也想不到更优秀的解法了, 实测数据并没有这么强, 这样的思路是可以通过的.

AC Code:

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#define N 1001
#define M 10001
#define C 101


int n, m, tot;
int q, c, s, e;
long long cost[C][N];
int price[N];
int head[N], nxt[M << 1], ver[M << 1], edge[M << 1];

struct State{
    long long res; // 当前花费
    int city;
    int fuel;
    bool operator < (const State& other) const {
        return res > other.res;
    }
};


int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch);  ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
    return f ? x : -x;
}

void add(int x, int y, int z){
    ver[++tot] = y, edge[tot] = z, nxt[tot] = head[x], head[x] = tot;
}

void solve(){
    memset(cost, 0x3f, sizeof(cost));
//    cost[s][0] = 0;
    cost[0][s] = 0;
    std::priority_queue<State> q;
    q.push({0, s, 0});
    while(q.size()){
        State x = q.top(); q.pop();
        if(x.res > cost[x.fuel][x.city]) continue;
        // 加油
        if(x.fuel < c){
            long long cur = x.res + price[x.city];
            if(cur < cost[x.fuel + 1][x.city]){
                cost[x.fuel + 1][x.city] = cur;
                q.push({cur, x.city, x.fuel + 1});
            }
        }
        // 走人
        for(int i = head[x.city]; i; i = nxt[i]){
            int y = ver[i], z = edge[i];
            if(x.fuel >= z){ // 油够
                if(x.res < cost[x.fuel - z][y]){
                    cost[x.fuel - z][y] = x.res;
                    q.push({x.res, y, x.fuel - z});
                }
            }
        }
    }
    long long ans = 1145141919810LL;
    for(int i = 0; i <= c; ++i) ans = std::min(ans, cost[i][e]);
    if(ans == 1145141919810LL) printf("impossible\n");
    else printf("%lld\n", ans);
}

int main(){
    n = read(), m = read();
    for(int i = 0; i < n; ++i) price[i] = read();
    for(int i = 1; i <= m; ++i){
        int u = read(), v = read(), w = read();
        add(u, v, w);
        add(v, u, w);
    } q = read();
    while(q--){
        c = read(), s = read(), e = read();
        solve();
    }
}
  • 标题: 程序设计实践 Week2 解题记录
  • 作者: Coast23
  • 创建于 : 2025-07-03 11:30:37
  • 更新于 : 2025-07-03 14:16:59
  • 链接: https://coast23.github.io/2025/07/03/程序设计实践-Week2-解题记录/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
目录
程序设计实践 Week2 解题记录
  1. 前言
  2. 1. 英杰们的蛋糕塔
  3. 2. 击杀黄金蛋糕人马
  4. 3. 寻找林克的回忆(1)
  5. 4. 寻找林克的回忆(2)
  6. 5. 寻找林克的回忆(4)
  7. 6. 寻找林克的回忆(4) [DLX]
  8. 7. 寻找林克的回忆(3)
  9. 8. 滚石柱
  10. 9. 维修电路
  11. 10. 最省赛程