程序设计实践 Week3 解题记录

程序设计实践 Week3 解题记录

Coast23
  2025-07-12 00:44:52 2025-07-12 00:44:52 创建   2025-07-12 01:22:22 2025-07-12 01:22:22 更新   7.8k 字  35 分钟  

前言

这周是 DP (Dynamic Programming, 动态规划) 入门.

因为 DP 是我的弱项, 所以这周的题目不再是选讲, 每题不论难易我都写了题解. 因为都是经典题目, 所以就不贴传送门了.

在进入题解环节前, 先聊聊我是如何理解 DP 的.

我对 DP 的个人理解是, 其核心思想在于将复杂问题分解为子问题, 这点和分治有点像, 但 DP 和分治不同的点在于, 分治的子问题往往是独立的 (比如归并排序, 分段之后左右两段的合并互不影响), 但 DP 面对的是大量重复的子问题 (以最简单的计算斐波那契数列为例, 计算 F(10) 需要 F(9) 和 F(8), 计算 F(9) 也需要 F(8), F(8) 被重复计算了), 此外, DP 往往还具有最优子结构, 即我们可以通过组合子问题的最优解来得到原问题的最优解, “状态转移方程” 就是最优子结构的数学体现. 此外, DP 还有一个重要的隐含前提, 就是无后效性, 也就是说, 一旦某个状态在当前确定了, 它就不能再被之后的阶段决策所影响.

(当然, 有些比较高级的 DP 可能并没有上述这样优良的性质, 不过这不在我们的讨论范围内, 因为我太菜了.)

总结一下, DP的本质就是: 利用最优子结构特性, 通过状态转移方程从子问题的解推导出全局解; 同时利用重叠子问题特性, 通过记忆化或列表法优化计算过程.

基于上面的本质, 我们可以得到 DP 问题的解题框架:

  1. 定义子问题 (状态). 一般是用数组 dp[i][j][...] 来表示, 其中等是用于决策的变量.
  2. 寻找状态转移方程. 这是 DP 的核心, 我很难总结出一套寻找状态转移方程的方法, 感觉更多都是 “瞪眼法” , 可能多做题就会了吧.
  3. 确定边界条件 (初始状态). 状态转移需要一个起点, 一般由题目初始条件给定.
  4. 提取答案. 从 dp 表中找出题目所要的答案, 没啥好多说的.

此篇文章的大部分题解都是按照这个框架写的.

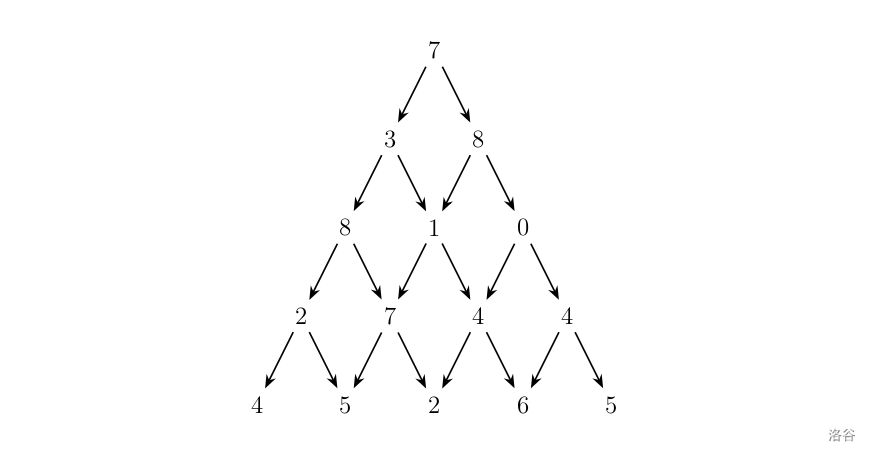
1. 数字三角形

题意简述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

示意图

在上面的样例中，从的路径产生了最大权值。

Solution

记 a[i][j]: 第行, 从左往右第个数字.
记 f[i][j]: 从走到的路径最大权值. 并令 f[i][0] = 0.

显然有:

  • f[1][1] = a[1][1]
  • f[i][j] = a[i][j] + max(f[i-1][j], f[i-1][j-1])

时间复杂度, 应该无法更优了.

代码略.

2. 林克的01背包

题意简述

给定个物品和背包容量, 每个物品具有体积与价值, 每个物品至多选一次, 求背包最多可以装多少价值的物品.

Solution

考虑子问题: 只取前个物品, 用容量为的背包, 最多可以凑出多少价值?

把这个子问题的答案记为 f[i][j] , 显然最终答案就是 f[N][M] .

接下来考虑转移, 显然, f[i][j] 由 f[i-1][*] 拓展而来, 若选择第个物品, 就有: f[i][j] = f[i-1][j - v[i]] + w[i], 若不选第个物品, 就有: f[i][j] = f[i-1][j].

于是, f[i][j] = max(f[i-1][j - v[i]] + w[i], f[i-1][j]) .

可以发现, f[i][*] 只与 f[i-1][*] 有关, 且当我们处理到时,已经处理好了, 所以这个数组的第一维其实是没用的, 我们可以直接用 f[j] 表示处理完当前物品后容量为的背包可装下的最大价值.

和上面一样, f[j] = max(f[j - v[i]] + w[i], f[j]) .

时间复杂度.
空间复杂度.

AC Code:

#include <cstdio>
#include <iostream>

int n, m;
int v[1005], w[1005];
int f[1005];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);
    return f ? x : -x;
}

int max(int a, int b){return a > b ? a : b;}

int main(){
	n = read(), m = read();
	for(int i = 1; i <= n; ++i) v[i] = read(), w[i] = read();
	for(int i = 1; i <= n; ++i){
		for(int j = m; j >= v[i]; --j){
			f[j] = max(f[j], f[j - v[i]] + w[i]);
		}
	}
	printf("%d\n", f[m]);
}

3. 林克的完全背包

题意简述

给定个物品和背包容量, 每个物品具有体积与价值, 每个物品无限件, 求背包最多可以装多少价值的物品.

Solution

和上一道 01背包 不一样了, 这题的物品不再是考虑 “选或不选” 这样的 “01” 选择, 而是要考虑每个物品的选择个数.

因此, 一个很朴素的想法是, 对于每个物品, 我都再加一层 for 循环来枚举它的选择个数. 这样的时间复杂度是的.

像上一题一样, 还是设 f[i][j] 表示只取前个物品, 用容量为的背包可凑出的最大价值.

于是, f[i][j] = max(f[i-1][j - v[i] * k] + w[i] * k) , 其中 k 表示第个物品的选择个数.

让我们思考一下, 我们真的需要枚举每个物品的选择个数 k 吗 ?

如果我们从小的往大的转移, 当我再考虑能否从 j - v[i] 转移到 j 的时候, j - v[i] * 2 能否转移到 j - v[i] 这个子问题必然已经被决策过了, 并且已经被记录到了 j - v[i] 这个状态中, 也就是说, 我们根本不需要用 j - v[i] * 2, j - v[i] * 3 … 来转移到 j, 因为这些情况已经被 j - v[i] 考虑过了! 它们属于重叠的子问题.

考虑完物品的个数, 再来考虑物品与物品间的转移, 容易发现这时的问题情景和01背包是一样的, 同样能够用滚动数组来减少一维状态. 完全背包问题 与 01背包问题 唯一的区别只有 j 的转移方向.

这样, 我们就把完全背包问题的时间复杂度降低到了, 空间复杂度降低到了.

AC Code:

#include <cstdio>
#include <iostream>

int n, m;
int v[1005], w[1005];
int f[1005];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);
    return f ? x : -x;
}

int max(int a, int b){return a > b ? a : b;}

int main(){
	n = read(), m = read();
	for(int i = 1; i <= n; ++i) v[i] = read(), w[i] = read();
	for(int i = 1; i <= n; ++i){
		for(int j = v[i]; j <= m; ++j){ // 只有枚举顺序的变化.
			f[j] = max(f[j], f[j - v[i]] + w[i]);
		}
	}
	printf("%d\n", f[m]);
}

4 & 5. 多重背包问题(1) & 多重背包问题(2)

题意简述

给定个物品和背包容量, 每个物品具有体积、价值以及件数, 求背包最多可以装多少价值的物品.

Solution

首先还是和完全背包的朴素做法一样, 去枚举每个物品的使用次数, 相当于把件相同物品当成不同物品, 然后用 01背包来解决, 时间复杂度. 这个时间复杂度的算法可以通过问题(1).

接下来考虑优化方式.

上面的做法有非常明显的问题, 如果我把第个物品拆成件, 那么同时选物品和与同时选物品和是等价的, 都是选件第个物品, 但类似的相同问题却被反复地考虑了.

我们肯定是不希望重复计算, 就要想办法来消除这种重复计算.

其实, 我们只关心第个物品选几件, 而非第个物品的第件物品选还是不选.

为了保证第个物品取件的这种情况能全部被考虑到, 我们就需要找到一种的拆分方式, 满足:

, 都可以通过的部分和来得到.

不难发现, 只需对进行二进制拆分即可, 比如:

像这样拆分即可. 然后再对拆分后的物品做 01背包.

时间复杂度.

AC Code:

#include <cstdio>
#include <iostream>

int n, m, cnt;
int v[1005], w[1005], s[1005];
int V[100005];
int W[100005];
int f[100005];

int read(){
	int x = 0, f = 1; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
	return f ? x : -x;
}

int max(int a, int b){return a > b? a : b;}

int main(){
	n = read(); m = read();
	for(int i = 1; i <= n; ++i){
		v[i] = read();
		w[i] = read();
		s[i] = read();
	}
	// 二进制拆分
	for(int i = 1; i <= n; ++i){
		int c = 1;
		while(s[i] > c){
			s[i] -= c;
			W[++cnt] = c * w[i];
			V[cnt] = c * v[i];
			c <<= 1;
		}
		W[++cnt] = s[i] * w[i];
		V[cnt] = s[i] * v[i];
	}
	for(int i = 1; i <= cnt; ++i){
		for(int j = m; j >= V[i]; --j){
			f[j] = max(f[j], f[j - V[i]] + W[i]);
		}
	}
	printf("%d\n", f[m]);
	return 0;
}

6. 分组背包问题

题意简述

给定组物品和背包容量, 每组物品有个, 第组 第件物品的体积为, 价值为, 每组物品只能选至多一件物品, 求背包最多可以装多少价值的物品.

Solution

既然是每组物品只能选至多一件物品, 那就对每组物品都做一个01背包.

为了保证只选至多一件物品, 对于当前组, 先从大到小枚举背包体积, 再枚举第件物品.

AC Code:

#include <cstdio>
#include <iostream>

int n, m;
int cnt[105];
int v[105][105];
int w[105][105];
int f[105];

int read(){
	int x = 0, f = 1; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
	return f ? x : -x;
}

int max(int a, int b){return a > b? a : b;}

int main(){
	n = read(), m = read();
	for(int i = 1; i <= n; ++i){
		cnt[i] = read();
		for(int j = 1; j <= cnt[i]; ++j){
			v[i][j] = read(), w[i][j] = read(); 
		}
	}
	for(int k = 1; k <= n; ++k){ // 哪一组
		for(int i = m; ~i; --i){ // 背包体积
			for(int j = 1; j <= cnt[k]; ++j){ // 对每个物品进行决策
				if(i >= v[k][j])
					f[i] = max(f[i], f[i-v[k][j]] + w[k][j]);
			}
		}
	}
	printf("%d\n", f[m]);
	return 0;
}

7. 混合背包问题

题意简述

有种物品和一个容量是的背包.

物品一共有三类:

  • 第一类物品只能用次（01背包）；
  • 第二类物品可以用无限次（完全背包）；
  • 第三类物品最多只能用次（多重背包）；

物品体积是，价值是。

求背包最多可以装多少价值的物品.

Solution

对前面三种背包类型题的综合应用.

只需要在枚举物品的时候, 根据物品的类型, 使用对应的状态转移方程即可.

AC Code:

#include <cstdio>
#include <iostream>

int n, m;
int s[1005], v[1005], w[1005];
int f[1005];

int read(){
	int x = 0, f = 1; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
	return f ? x : -x;
}

int max(int a, int b){return a > b? a : b;}

int main(){
	n = read(), m = read();
	for(int i = 1; i <= n; ++i){
		v[i] = read(), w[i] = read(), s[i] = read();
	}
	for(int i = 1; i <= n; ++i){
		if(s[i] == -1){ // 01 背包
			for(int j = m; j >= v[i]; --j) f[j] = max(f[j], f[j-v[i]] + w[i]);
		}
		else if(s[i] == 0){ // 完全背包
			for(int j = v[i]; j <= m; ++j) f[j] = max(f[j], f[j-v[i]] + w[i]);
		}
		else{ // 多重背包
			for(int j = m; j >= v[i]; --j){
				for(int k = 1; j >= k * v[i] and k <= s[i]; ++k){
					f[j] = max(f[j], f[j-k*v[i]] + k*w[i]);
				}
			}
		}
	}
	printf("%d\n", f[m]);
	return 0;
}

8. 摘花生

题意简述

给定一个行,列的网格, 每个格点有分数. 从左上角走到右下角, 每次只能向下或向右走, 最大化走过的格点分数和.

参考图

Solution

和数字三角形是一样的.

记 f[i][j] 表示走到的最大分数, 于是有如下转移方程:

初始条件:.

答案:.

注意边界可能需要特殊的处理.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>

int T, n, m;
int a[105][105];
int f[105][105];

int read(){
	int x = 0, f = 1; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
	return f ? x : -x;
}

int max(int a, int b){return a > b? a : b;}

void solve(){
	memset(f, 0, sizeof(f));
	n = read(); m = read();
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= m; ++j)
			a[i][j] = read();
	f[1][1] = a[1][1];
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= m; ++j){
			if(i == 1 and j == 1) continue;
			if(i == 1) f[i][j] = max(f[i][j], f[i][j-1] + a[i][j]);
			if(j == 1) f[i][j] = max(f[i][j], f[i-1][j] + a[i][j]);
			if(i > 1 and j > 1){
				f[i][j] = max(f[i][j], f[i-1][j] + a[i][j]);
				f[i][j] = max(f[i][j], f[i][j-1] + a[i][j]);
			}
		}
	}
	printf("%d\n", f[n][m]);
}

int main(){
	T = read();
	while(T--) solve();
	return 0;
}

9. 最低通行费

题意简述

和上一题一样, 但这次是要最小化正方形网格图的分数和.

Solution

状态转移方程把 max 改成 min 即可, 然后初始时 f[][] 要设为.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>

int T, n, m;
int a[105][105];
int f[105][105];

int read(){
	int x = 0, f = 1; char ch = getchar();
	for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
	return f ? x : -x;
}

int min(int a, int b){return a < b? a : b;}

void solve(){
	memset(f, 0x3f, sizeof(f));
//	n = read(); m = read();
	n = m = read();
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= m; ++j)
			a[i][j] = read();
	f[1][1] = a[1][1];
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= m; ++j){
			if(i == 1 and j == 1) continue;
			if(i == 1) f[i][j] = min(f[i][j], f[i][j-1] + a[i][j]);
			if(j == 1) f[i][j] = min(f[i][j], f[i-1][j] + a[i][j]);
			if(i > 1 and j > 1){
				f[i][j] = min(f[i][j], f[i-1][j] + a[i][j]);
				f[i][j] = min(f[i][j], f[i][j-1] + a[i][j]);
			}
		}
	}
	printf("%d\n", f[n][m]);
}

int main(){
//	T = read();
	T = 1;
	while(T--) solve();
	return 0;
}

10 & 11. 最长上升子序列 & 最长上升子序列(2)

题意简述

给定一个长度为的数列, 求数值严格单调递增的子序列的长度最长是多少.

Solution

设 f[i] 表示以 A[i] 结尾的最长上升子序列的长度.

然后, 要求的时候, 我们就回头找, 如果, 就尝试把放到这个子序列的后面, 也就是令.

很容易写出这个思路对应的状态转移方程:

.

时间复杂度.

参考代码:

#include <cstdio>
#include <iostream>

int n;
int a[1005];
int f[1005]; // 以 f[i] 结尾的最长上升子序列的长度

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
    return f ? x : -x;
}

int max(int a, int b){return a > b? a : b;}

int main(){
	n = read();
	for(int i = 1; i <= n; ++i) a[i] = read(), f[i] = 1;
	int ans = 1;
	for(int i = 2; i <= n; ++i){
		for(int j = 1; j < i; ++j){
			if(a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
		}
		ans = max(ans, f[i]);
	}
	printf("%d\n", ans);
}

其实我的第一反应并不是这样.

题目要求最长上升子序列, 那我们就直接维护最长上升子序列 不就行了 ?

用 f[k] 表示长度为 k 的最长上升子序列的末尾元素最小值. 那么, f[k] 必然是一个单调递增的数组.

从左到右扫描, 如果大于, 说明能够加在原来以结尾的最长上升子序列的后面, 于是令.

否则, 就尝试用更新原来的. 我们需要找到中的一个位置, 这个位置满足:

比原来的更优是第一个可被更新的元素

怎么找这个呢? 因为是单调递增的, 所以可以直接二分查找, 用 lower_bound 即可.

时间复杂度.

AC Code:

#include <cstdio>
#include <iostream>
#include <algorithm>

int n;
int a[100005];
int f[100005];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);
    return f ? x : -x;
}

int max(int a, int b){return a > b? a : b;}

int main(){
	n = read();
	for(int i = 1; i <= n; ++i) a[i] = read();
	f[1] = a[1]; int len = 1;
	for(int i = 2; i <= n; ++i){
		if(a[i] > f[len]) f[++len] = a[i];
		else *std::lower_bound(&f[1], &f[len+1], a[i]) = a[i];
	}
	printf("%d\n", len);
}

12. 拦截导弹

题目描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度，计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

简述一下题意:

给定一个长为的序列, 求:

  • 最长不下降子序列的长度;
  • 覆盖整个序列的不下降子序列的最少个数.
Solution

对于第一问, 我们依旧是用求最长上升子序列的方法, 用 f[k] 表示长度为 k 的最长不下降子序列的末尾元素最大值. 那么, f[k] 必然是一个单调不减的数组.

依旧是从左到右扫描, 如果小于等于, 说明能够加在原来以结尾的最长不下降序列的后面, 于是令.

否则, 就尝试用更新原来的. 我们需要找到中的一个位置, 这个位置满足:

比原来的更优是第一个可被更新的元素

最后的就是最长不下降子序列的最大长度.

再来看看这个令人头疼的第二问, 这里需要用到 Dilworth 定理:

「偏序集能划分成的最少的全序集个数等于最大反链的元素个数.」

也就是:

[覆盖整个序列的最长不下降子序列的最少个数] 等于 [最长上升子序列的长度].

定理的详细介绍请翻阅 OI-Wiki, 我这里不展开, 直接当结论用.

知道这个结论, 这道题就容易解决了. 分别求最长不下降子序列的长度和最长上升子序列的长度即可.

时间复杂度.

AC Code:

#include <cstdio>
#include <iostream>
#include <algorithm>
#define N 30005

int n, len1, len2;
int a[N];
int LNDS[N], LIS[N];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
    return f ? x : -x;
}

int& bsearch(int l, int r, int x){
    int res = l;
    while(l <= r){
        int mid = (l + r) >> 1;
        if(LNDS[mid] < x) res = mid, r = mid - 1;
        else l = mid + 1;
    }
    return LNDS[res];
}

int main(){
    while(~scanf("%d", &a[n+1])) ++n;
    len1 = 1, len2 = 1;
    LNDS[1] = a[1];
    LIS[1] = a[1];
    for(int i = 2; i <= n; ++i){
        // 处理最长不下降子序列
        if(LNDS[len1] >= a[i]) LNDS[++len1] = a[i];
        else bsearch(1, len1, a[i]) = a[i];

        // 处理最长上升子序列
        if(LIS[len2] < a[i]) LIS[++len2] = a[i];
        else *std::lower_bound(&LIS[1], &LIS[len2+1], a[i]) = a[i];
    }
    printf("%d\n%d\n", len1, len2);
}

13. 最长公共子序列

题意简述

给定两个长度分别为和的字符串 A 和 B ，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。

Solution

记 f[i][j] 表示以 A[i] , B[j] 为结尾的最长公共子序列的长度.

转移方程:

用变量 ans 记录 f[i][j] 中的最大值, 此即为最长公共子序列的长度.

时间复杂度.

AC Code:

#include <cstdio>
#include <iostream>

int n, m, ans;
char A[1003];
char B[1003];
int f[1003][1003]; // f[i][j]: 以 A[i] 和 B[j] 结尾的最长公共子序列的长度


int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);
    return f ? x : -x;
}

int max(int a, int b){return a > b? a : b;}

int main(){
	n = read(), m = read();
	std::cin >> A + 1 >> B + 1;
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= m; ++j){
			if(A[i] == B[j]) f[i][j] = f[i-1][j-1] + 1;
			else f[i][j] = max(f[i-1][j], f[i][j-1]);
			ans = max(ans, f[i][j]);
		}
	}
	printf("%d\n", ans);
}

14. 石子合并

题意简述

设有堆石子排成一排，其编号为。每堆石子有一定的质量。现在要将这堆石子合并成为一堆。每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻。合并时由于选择的顺序不同，合并的总代价也不相同。试找出一种合理的方法，使总的代价最小，并输出最小代价。

Solution

如果是合并任意两堆, 那就是贪心, 也就是构造 Huffman 树.

但如果是合并相邻两堆, 那就是 区间DP 了.

设 f[i][j] 表示将区间合并为一堆, 所需的最小代价.

那么, 就枚举这个区间里的某堆石子表示 “分隔点”, 即表示区间由区间与合并而来.

很容易得到状态转移方程:

其中表示前缀和

接下来要思考转移顺序.

显然, 大区间由小区间合并而来, 所以我们要先计算出小区间, 再计算大区间.

所以, 以作为阶段, 先从小到大枚举, 再枚举, 计算出后再枚举进行转移.

初始条件:.
答案即为:.

时间复杂度.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>
#define N 302

int n;
int a[N];
int sum[N];
int f[N][N];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
    return f ? x : -x;
}

int min(int a, int b){return a < b? a : b;}

int main(){
    memset(f, 0x3f, sizeof(f));
    n = read();
    for(int i = 1; i <= n; ++i) a[i] = read(), f[i][i] = 0, sum[i] = sum[i-1] + a[i];
    for(int len = 2; len <= n; ++len){
        for(int i = 1; i <= n - len + 1; ++i){
            int j = i + len - 1;
            for(int k = i; k < j; ++k){
                f[i][j] = min(f[i][j], f[i][k] + f[k+1][j] + sum[j] - sum[i-1]);
            }
        }
    }
    printf("%d\n", f[1][n]);
    return 0^(0-0)^0;
}

15. 环形石子合并

题意简述

在一个圆形操场的四周摆放堆石子，现要将石子有次序地合并成一堆，规定每次只能选相邻的堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将堆石子合并成堆的最小得分和最大得分。

Solution

上一题是区间为链的情况, 这一题是区间为环的情况.

最直接的想法就是把环变成链.

我能想到的做法有这两种:

  • 枚举把环切开的位置, 切开后就是上一道题的情况了, 由于有种分开环的方法, 所以时间复杂度是.
  • 把原来的链复制一遍, 即在原来链的基础上, 令, 对这个长为的链做区间DP, 最后的答案即为中的最大值和最小值. 时间复杂度是.

我选择第二种倍长链的做法.

AC Code:

#include <cstdio>
#include <cstring>
#include <iostream>
#define N 202

int n;
int a[N << 1];
int sum[N << 1];
int fmin[N << 1][N << 1];
int fmax[N << 1][N << 1];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
    return f ? x : -x;
}

int min(int a, int b){return a < b? a : b;}
int max(int a, int b){return a > b? a : b;}

int main(){
    memset(fmin, 0x3f, sizeof(fmin));
    memset(fmax, -0x3f, sizeof(fmax));
    n = read();
    for(int i = 1; i <= n; ++i) a[i] = read(), a[i+n] = a[i];
    for(int i = 1; i <= n << 1; ++i) sum[i] = sum[i-1] + a[i], fmin[i][i] = 0, fmax[i][i] = 0;
    for(int len = 2; len <= n; ++len){
        for(int i = 1; i <= (n << 1) - len + 1; ++i){
            int j = i + len - 1;
            for(int k = i; k < j; ++k){
                fmin[i][j] = min(fmin[i][j], fmin[i][k] + fmin[k+1][j] + sum[j] - sum[i-1]);
                fmax[i][j] = max(fmax[i][j], fmax[i][k] + fmax[k+1][j] + sum[j] - sum[i-1]);
            }
        }
    }
    fmin[0][0] = 0x3f3f3f3f, fmax[0][0] = -0x3f3f3f3f;
    for(int i = 1; i <= n; ++i){
        fmin[0][0] = min(fmin[0][0], fmin[i][i+n-1]);
        fmax[0][0] = max(fmax[0][0], fmax[i][i+n-1]);
    }
    printf("%d\n%d\n", fmin[0][0], fmax[0][0]);
    return 0^(0-0)^0;
}

16. 加分二叉树

题意简述

设一个个节点的二叉树的中序遍历为，其中数字为节点编号。每个节点都有一个分数（均为正整数），记第个节点的分数为，及它的每个子树都有一个加分，任一棵子树（也包含本身）的加分计算方法如下：

的左子树的加分的右子树的加分的根的分数。

若某个子树为空，规定其加分为，叶子的加分就是叶节点本身的分数。不考虑它的空子树。

试求一棵符合中序遍历为且加分最高的二叉树。要求输出

  1. 的最高加分。
  2. 的前序遍历。
Solution

二叉树的中序遍历就是这棵树从左往右看的顺序, 而且它有这样的性质:

可以用区间描述一棵子树, 这棵子树的 “最左边的点” 就是, “最右边的点” 就是.

此外, 根节点也必定在, 我们不妨设根节点为.

那么, 对于以为根的子树, 它的左子树的区间就为, 它的右子树的区间就为. (或表示相应的子树为空.)

同时, 容易发现子树的分数只对有直接贡献, 因此我们可以设表示子树的分数, 根据题意, 有如下转移方程:

初始时有, 答案即为.

而题目还要求给出最优树的先序遍历, 这个也简单, 可以用数组记录区间的根节点, 在转移的时候一起更新即可.

别忘了初始时有.

AC Code:

/*
    f[l][r]: max subtree of [l, r]
    f[l][r] = max {f[l][k-1] * f[k+1][r] + f[k][k], k∈[l, r]}
    init():
        f[i][i] = t[i]
        root[i][i] = i
*/
#include <cstdio>
#include <iostream>
#define N 31

int n;
int d[N];
int root[N][N];
long long f[N][N];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch xor 48);
    return f ? x : -x;
}

long long dfs(int l, int r){
    if(l == r) return d[l];
    if(f[l][r]) return f[l][r];
    if(l > r) return 1; // 空子树加分为 1
    for(int i = l; i <= r; ++i){ // 枚举可能的根
        long long res = dfs(l, i - 1) * dfs(i + 1, r) + f[i][i];
        if(res > f[l][r]){
            f[l][r] = res;
            root[l][r] = i;
        }
    }
    return f[l][r];
}

void print(int l, int r){
    // 根 - 左 - 右
    if(l > r) return;
    printf("%d ", root[l][r]);
    print(l, root[l][r] - 1);
    print(root[l][r] + 1, r);
}

int main(){
    n = read();
    for(int i = 1; i <= n; ++i) d[i] = read(), f[i][i] = d[i], root[i][i] = i;
    printf("%lld\n", dfs(1, n));
    print(1, n);
    return 0^(0-0)^0;
}

17. 树形DP之树的最长路径

题意简述

给定一棵树, 包含个节点和条带权无向边, 求树的最长路.

Solution

对于以为根的子树, 如果这个子树有部分属于最长路, 那么一定在最长路上, 而且:

  • 的所有子树中的最长链必定属于最长路.
  • 的所有子树中的次长链可能属于最长路. (因为最长路也可能往的父亲方向走)

那么, 就可以以函数 dfs(x) 表示以为根的子树的最长链的权值和, 从根节点往下搜, 每次都递归求出最长链和次长链, 并更新全局最长链长度, 最后返回该子树的最长链即可.

AC Code:

#include <cstdio>
#include <iostream>
#define N 10004

int n, tot;
int ans;
int ver[N << 1], edge[N << 1], nxt[N << 1], head[N];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);
    return f ? x : -x;
}

void add(int x, int y, int z){
	ver[++tot] = y, edge[tot] = z, nxt[tot] = head[x], head[x] = tot;
}

int max(int a, int b){return a > b? a : b;}

int dfs(int x, int fa){
	int d1 = 0, d2 = 0;
	for(int i = head[x]; i; i = nxt[i]){
		int y = ver[i]; if(y == fa) continue;
		int d = dfs(y, x) + edge[i];
		if(d >= d1) d2 = d1, d1 = d;
		else if(d > d2) d2 = d;
	}
	ans = max(ans, d1 + d2);
	return d1;
}

int main(){
	n = read();
	for(int i = 1; i < n; ++i){
		int u = read(), v = read(), w = read();
		add(u, v, w); add(v, u, w);
	}
	dfs(1, 0);
	printf("%d\n", ans);
}

18. 没有上司的舞会

题意简述

某大学有个职员，编号为。

他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。

现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。

所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

Solution
  • 以 f[x][0] 表示 x 不参加的情况下, 以 x 为根的子树的最大快乐指数
  • 以 f[x][1] 表示 x 参加的情况下, 以 x 为根的子树的最大快乐指数

显然有如下转移方程:

初始条件:.
答案:

AC Code:

#include <cstdio>
#include <iostream>
#define N 6005

int n, tot, ans;
int a[N], f[N][2];
int ver[N], nxt[N], head[N], in[N];

int read(){
    int x = 0, f = 1; char ch = getchar();
    for(; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
    for(; isdigit(ch); ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);
    return f ? x : -x;
}

void add(int x, int y){
	ver[++tot] = y, ++in[y], nxt[tot] = head[x], head[x] = tot;
}

int max(int a, int b){return a > b ? a : b;}

void dfs(int x, int fa){
	for(int i = head[x]; i; i = nxt[i]){
		int y = ver[i]; if(y == fa) continue;
		dfs(y, x);
		f[x][1] += f[y][0];
		f[x][0] += max(f[y][0], f[y][1]);
	}
}

int main(){
	n = read();
	for(int i = 1; i <= n; ++i) a[i] = read(), f[i][1] = a[i];
	for(int i = 1; i < n; ++i){
		int u = read();/* add(u, read()); */
		add(read(), u);
	}
	for(int i = 1; i <= n; ++i){
		if(!in[i]){
			dfs(i, 0);
			return printf("%d\n", max(f[i][0], f[i][1])) & 0;
		}
	}
}
  • 标题: 程序设计实践 Week3 解题记录
  • 作者: Coast23
  • 创建于 : 2025-07-12 00:44:52
  • 更新于 : 2025-07-12 01:22:22
  • 链接: https://coast23.github.io/2025/07/12/程序设计实践-Week3-解题记录/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
目录
程序设计实践 Week3 解题记录
  1. 前言
  2. 1. 数字三角形
  3. 2. 林克的01背包
  4. 3. 林克的完全背包
  5. 4 & 5. 多重背包问题(1) & 多重背包问题(2)
  6. 6. 分组背包问题
  7. 7. 混合背包问题
  8. 8. 摘花生
  9. 9. 最低通行费
  10. 10 & 11. 最长上升子序列 & 最长上升子序列(2)
  11. 12. 拦截导弹
  12. 13. 最长公共子序列
  13. 14. 石子合并
  14. 15. 环形石子合并
  15. 16. 加分二叉树
  16. 17. 树形DP之树的最长路径
  17. 18. 没有上司的舞会